Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\left(E\right):\dfrac{x^2}{100}+\dfrac{y^2}{36}=1\)
b) \(\left(E\right):\dfrac{x^2}{169}+\dfrac{y^2}{25}=1\)

a) \(\left(E\right):\dfrac{x^2}{5}+\dfrac{y^2}{4}=1\)
b) \(\left(E\right):\dfrac{x^2}{25}+\dfrac{y^2}{16}=1\)

Phương trình chính tắc của elip có dạng :
+
= 1
a) Ta có a > b :
2a = 8 => a = 4 => a2 = 16
2b = 6 => b = 3 => b2 = 9
Vậy phương trình chính tắc của elip có dạng +
= 1
b) Ta có: 2a = 10 => a = 5 => a2 = 25
2c = 6 => c = 3 => c2 = 9
=> b2 = a2 – c2 => b2 = 25 – 9 = 16
Vậy phương trình chính tắc của elip có dạng +
= 1

Phương trình chính tắc của elip có dạng :
+
= 1
a) Ta có a > b :
2a = 8 => a = 4 => a2 = 16
2b = 6 => b = 3 => b2 = 9
Vậy phương trình chính tắc của elip có dạng +
= 1
b) Ta có: 2a = 10 => a = 5 => a2 = 25
2c = 6 => c = 3 => c2 = 9
=> b2 = a2 – c2 => b2 = 25 - 9 = 16
Vậy phương trình chính tắc của elip có dạng +
= 1.

a, Phương trình chính tắc của (E) có dạng
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) với 0<b<a
Ta có A(0;2) \(\in\left(E\right)\)<=>b=2
(E) có tiêu điểm F1\(\left(-\sqrt{5};0\right)\) => c=\(\sqrt{5}\)
Ta có \(a^2=b^2+c^2=4+5=9\)=>a=3
==> (E) \(\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)
b, 2a = 6; 2b = 4; 2c = \(2\sqrt{5}\)=>\(\dfrac{c}{a}=\dfrac{\sqrt{5}}{3}\)
c, S=4ab=24

Độ dài trục lớn bằng 10 ⇒ 2a = 10 ⇒ a = 5
Tiêu cự bằng 6 ⇒ 2c = 6 ⇒ c = 3
⇒ b2 = a2 – c2 = 16 ⇒ b = 4.
Vậy phương trình chính tắc của Elip là: 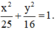

a) Từ giả thiết ta có \(a = 5,b = 4\)
Suy ra phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
b) Ta có: \(a = 5,c = 3 \Rightarrow b = \sqrt {{a^2} - {c^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Suy ra phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
c) Từ giả thiết ta có: \(2a = 16,2b = 12 \Rightarrow a = 8,b = 6\)
Suy ra phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{36}} = 1\)
d) Từ giả thiết ta có: \(2a = 20,2c = 12 \Rightarrow a = 10,c = 6 \Rightarrow b = \sqrt {{a^2} - {c^2}} = \sqrt {{{10}^2} - {6^2}} = 8\)
Suy ra phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\)

a/ \(2a=10\Rightarrow a=5\Rightarrow a^2=25\)
\(2c=6\Rightarrow c=3\Rightarrow b^2=a^2-c^2=25-9=16\)
Phương trình elip: \(\frac{x^2}{25}+\frac{y^2}{16}=1\)
b/ \(c=\sqrt{3}\Rightarrow c^2=3\)
Gọi pt elip có dạng \(\frac{x^2}{a^2}+\frac{y^2}{a^2-3}=1\)
Do điểm \(\left(1;\frac{\sqrt{3}}{2}\right)\) thuộc elip nên \(\frac{1}{a^2}+\frac{3}{4\left(a^2-3\right)}=1\)
\(\Leftrightarrow4\left(a^2-3\right)+3a^2=4a^2\left(a^2-3\right)\)
\(\Leftrightarrow4a^4-19a^2+12=0\Rightarrow\left[{}\begin{matrix}a^2=4\\a^2=\frac{3}{4}< c^2\left(l\right)\end{matrix}\right.\)
Vậy pt elip là: \(\frac{x^2}{4}+\frac{y^2}{1}=1\)