HO
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
5
5 tháng 4 2018
Ví dụ 2x+7-5= 28
=> 2x+7=28-5
=>2x+7=23
=>2x =23-7
=>2x =16
=>x =16:2
=> x =8
NK
5
15 tháng 1 2018
?1 :
a) Điểm -5 nằm ..bên trái.. điểm -3, nên -5 < -3, và viết : -5 < -3.
b) Điểm 2 nằm ..bên phải.. điểm -3, nên 2 > -3, và viết : 2 > -3.
c) Điểm -2 nằm ..bên trái.. điểm 0, nên -2 < 0, và viết : -2 < 0.
15 tháng 1 2018
Vì phần tử của A là số tự nhiên lớn hơn 8 và nhỏ hơn 14 không thuoccj tập hợp A
Vậy A = { 9 ; 10 ; 11 ; 12 ; 13 }
Dùng tính chất đặc trưng cho các phần tử
\(A=\left\{x\in N,8< x< 14\right\}\)
Ta có : \(12\in A\)và \(16\notin A\)
HO
2
30 tháng 3 2017
A=\(\dfrac{7}{19}\).\(\left(\dfrac{8}{11}+\dfrac{3}{11}\right)\)+\(\dfrac{12}{19}\)
A=\(\dfrac{7}{19}.1+\dfrac{12}{19}\)
A= \(\dfrac{7}{19}+\dfrac{12}{19}=1\)
B=\(\dfrac{5}{9}.\left(\dfrac{7}{13}+\dfrac{9}{13}-\dfrac{3}{13}\right)\)
B=\(\dfrac{5}{9}.1=\dfrac{5}{9}\)
21 tháng 2 2021
Bài 37 trang 11 sách bài tập Toán 6 Tập 2: Bạn Minh đã tìm ra một cách "rút gọn" phân số rất đơn giản. Này nhé:
Em hãy kiểm tra xem các kết quả tìm được có đúng không?
Em có thể áp dụng "phương pháp" này để rút gọn các phân số có dạng ab/bc hay không?
Lời giải:
Kiểm tra ta thấy các kết quả tìm được đều đúng. Tuy nhiên, không thể áp dụng "phương pháp" trên để rút gọn các phân số có dạng ab/bc.
Ví dụ : 
Cách "rút gọn" của bạn Minh chỉ đúng một cách ngẫu nhiên
HO
1
12 tháng 4 2017
a) Bạn Cường đã đổi hỗn số sang phân số rồi cộng các phân số sau đó đổi kết quả sang hỗn số.
b) Cách tính nhanh hơn là: Cộng riêng phần nguyên cộng riêng phần phân số.
NL
5
9 tháng 2 2017
a)
- Vì 84 và 180 cùng chia hết cho x nên x là ƯC(84, 180). - Tìm ƯC(84, 180) thông qua tìm ƯCLN(84, 180) + Phân tích: 84 = 22.3.7 180 = 22.32.5 + Các thừa số chung là 2, và 3 + Số mũ nhỏ nhất của 2 là 2, của 3 là 1. Do đó ƯCLN(84, 180) = 22.3 = 12 Suy ra ƯC(84, 180) = {1, 2, 3, 4, 6, 12} - Vì x > 6 nên x = 12
Vậy A = {12}
b)
- Vì x chia hết cho cả 12, 15 và 18 nên x là BC(12, 15, 18). - Tìm BC(12, 15, 18) thông qua tìm BCNN(12, 15, 18) + Phân tích: 12 = 22.3 15 = 3.5 18 = 2.32 + Chọn thừa số chung, riêng: đó là 2, 3, 5 + Số mũ lớn nhất của 2 và 3 là 2, của 5 là 1. Do đó BCNN(12, 15, 18) = 22.32.5 = 180 Suy ra BC(12, 15, 18) = {0, 180, 360, 540, ...} - Vì 0 < x < 300 nên x = 180
Vậy B = {180}
9 tháng 2 2017
a)
- Vì 84 và 180 cùng chia hết cho x nên x là ƯC(84, 180). - Tìm ƯC(84, 180) thông qua tìm ƯCLN(84, 180) + Phân tích: 84 = 22.3.7 180 = 22.32.5 + Các thừa số chung là 2, và 3 + Số mũ nhỏ nhất của 2 là 2, của 3 là 1. Do đó ƯCLN(84, 180) = 22.3 = 12 Suy ra ƯC(84, 180) = {1, 2, 3, 4, 6, 12} - Vì x > 6 nên x = 12
Vậy A = {12}
b)
- Vì x chia hết cho cả 12, 15 và 18 nên x là BC(12, 15, 18). - Tìm BC(12, 15, 18) thông qua tìm BCNN(12, 15, 18) + Phân tích: 12 = 22.3 15 = 3.5 18 = 2.32 + Chọn thừa số chung, riêng: đó là 2, 3, 5 + Số mũ lớn nhất của 2 và 3 là 2, của 5 là 1. Do đó BCNN(12, 15, 18) = 22.32.5 = 180 Suy ra BC(12, 15, 18) = {0, 180, 360, 540, ...} - Vì 0 < x < 300 nên x = 180
Vậy B = {180}
AA
1
15 tháng 9 2016
a) Số dư trong phép chia một số tự nhiên cho số tự nhiên b ≠ 0 là một số tự nhiên r < b nghĩa là r có thể là 0; 1;...; b - 1.
Số dư trong phép chia cho 3 có thể là 0; 1; 2.
Số dư trong phép chia cho 4 có thể là: 0; 1; 2; 3.
Số dư trong phép chia cho 5 có thể là: 0; 1; 2; 3; 4.
b) Dạng tổng quát của số tự nhiên chia hết cho 3 là 3k, với k ∈ N.
Dạng tổng quát của số tự nhiên chia hết cho 3, dư 1 là 3k + 1, với k ∈ N.
Dạng tổng quát của số tự nhiên chia hết cho 3, dư 2 là 3k + 2, với k ∈ N.
27 tháng 3 2016
mik mới làm trang 43 chưa hox trang 50
10 tháng 2 2017
a) 15 tổng.
b) 7 tổng chia hết cho 2
Chúc bạn may mắn và xinh đẹp hơn nhé!
10 tháng 2 2017
a)
Do A có 5 phần tử, B có 3 phần tử nên ta có thể thiết lập được:
5.3 = 15 tổng dạng (a + b)
b) Tổng chia hết cho 2 là các tổng chẵn, ta có:
- A có 3 phần tử chẵn, B có 1 phần tử chẵn nên ta có 3.1 tổng chẵn.
- A có 2 phần tử lẻ, B có 2 phần tử lẻ nên ta có 2.2 tổng chẵn.
Tổng cộng ta có: 3.1 + 2.2 = 7 tổng chẵn.
Vậy trong các tổng trên, có 7 tổng chia hết cho 2.
MÌNH LÀM THẾ ĐÚNG KHÔNG . NẾU ĐÚNG MÌNH LẠI HỨA 100000%
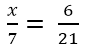
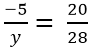
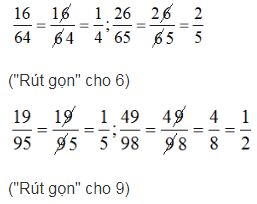
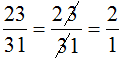
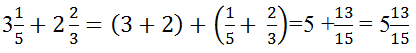
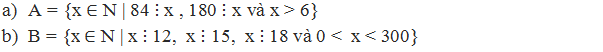
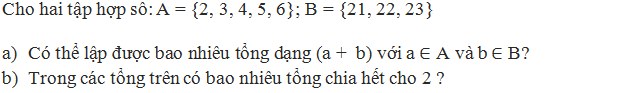
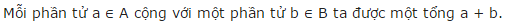
ví dụ :7/3 và 7/4
Bài 72 (trang 37 SGK Toán 6 tập 2):
Đố: Có những cặp phân số mà ta nhân chúng với nhau hoặc cộng chúng với nhau đều được cùng một kết quả.
Giải:
Giả sử ta chọn hai phân số có cùng tử: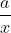
và 
.
Ta muốn có
.
Thế thì a . a = a.(x + y). Từ đó suy ra x + y = a.
Vì vậy với mỗi a > 1 cho trước ta có thể chọn x và y sao cho x + y = a.
Chẳng hạn với a = 11, x = 5, y = 6 ta có:
Mặt khác,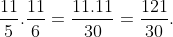
Vậy 
.
Như vậy ta có thể tìm được vô số cặp phân số mà tổng và tích của chúng bằng nhau.