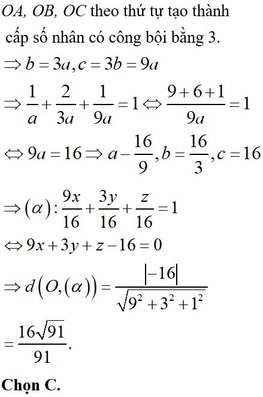Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì tia Ot là tia phân giác của \(\widehat{xOy}\)
=> \(\widehat{xOt}=\widehat{yOt}=\dfrac{\widehat{xOy}}{2}=\dfrac{70^o}{2}=35^o\)
Vậy \(\widehat{yOt}=35^o\)
b) Trên cùng 1 nửa mặt phẳng bờ chứa tia Ox có :
\(\widehat{xOy}=70^o< \widehat{xOz}=90^o\)
=> Tia Oy nằm giữa tia Ox và tia Oz
=> \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\left(1\right)\)
Thay \(\widehat{xOy}=70^o\) và \(\widehat{xOz}=90^o\) vào (1) , ta được :
\(70^o+\widehat{yOz}=90^o\)
=> \(\widehat{yOz}=90^o-70^o=20^o\)
Vậy \(\widehat{yOz}=20^o\)
Cặp góc phụ nhau có trong hình là \(\widehat{xOy}\) và \(\widehat{yOz}\)

Đáp án C
Phương pháp: Sử dụng phương pháp xác định tâm mặt cầu ngoại tiếp khối chóp.
Cách giải: Đặt A(x;0;0), B(0;y;0), (x,y > 0)
Vì OA + OB = OC = 1 => x + y = 1
Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G.
∆OAB vuông tại O => J là tâm đường tròn ngoại tiếp tam giác.
GJ // OC => GJ ⊥ (OAB) => GO = GA = GB
GF // JO, JO ⊥ OC => GF ⊥ OC, mà F là trung điểm của OC
=>GF là đường trung trực của OC => GC = GO
=> GO = GA = GB = GC => G là tâm mặt cầu ngoại tiếp tứ diện OABC
Bán kính mặt cầu ngoại tiếp tứ diện OABC :
![]()
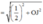
Ta có:
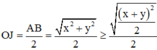
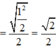
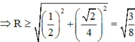
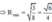

Trên nửa mặt phẳng có bờ chứa tia Ox, vẽ tia Oy, Oz sao cho ∠xOy = 50 độ; ∠xOy = 100 độ Sai đề

Bài 3:
Do a và b đều không chia hết cho 3 nhưng khi chia cho 3 thì có cùng số dư nên\(\left[{}\begin{matrix}\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\\\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\end{matrix}\right.\)
TH1:\(\left\{{}\begin{matrix}a=3n+1\\b=3m+1\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+1\right)\left(3m+1\right)-1\)
\(\Rightarrow ab-1=9nm+3m+3n+1-1=9nm+3m+3n⋮3\) nên là bội của 3 (đpcm)
TH2:\(\left\{{}\begin{matrix}a=3n+2\\b=3m+2\end{matrix}\right.\)
\(\Rightarrow ab-1=\left(3n+2\right)\left(3m+2\right)-1\)
\(\Rightarrow ab-1=9nm+6m+6n+4-1=9nm+6m+6n+3⋮3\) nên là bội của 3 (đpcm)
Vậy ....
Bài 2:
\(B=\frac{1}{2010.2009}-\frac{1}{2009.2008}-\frac{1}{2008.2007}-...-\frac{1}{3.2}-\frac{1}{2.1}\)
\(\Rightarrow B=\frac{1}{2010.2009}-\left(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\right)\)
Đặt A=\(\frac{1}{2009.2008}+\frac{1}{2008.2007}+...+\frac{1}{3.2}+\frac{1}{2.1}\)
\(\Rightarrow A=\frac{2009-2008}{2009.2008}+\frac{2008-2007}{2008.2007}+...+\frac{3-2}{3.2}+\frac{2-1}{2.1}\)
\(\Rightarrow A=\frac{2-1}{2.1}+\frac{3-2}{3.2}+...+\frac{2008-2007}{2008.2007}+\frac{2009-2008}{2009.2008}\)
\(\Rightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2007}-\frac{1}{2008}+\frac{1}{2008}-\frac{1}{2009}\)
\(\Rightarrow A=1-\frac{1}{2009}\)
\(\Rightarrow B=\frac{1}{2010.2009}-A=\frac{1}{2010.2009}-\left(1-\frac{1}{2009}\right)\)
\(\Rightarrow B=\frac{1}{2010.2009}+\frac{1}{2009}-1=\frac{2011}{2010.2009}-1\)

Bài 7:
a: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOy}< \widehat{xOt}\)
nên tia Oy nằm giữa hai tia Ox và Ot
b: Ta có: tia Oy nằm giữa hai tia Ox và Ot
mà \(\widehat{xOy}=\dfrac{1}{2}\widehat{xOt}\)
nên Oy là tia phân giác của góc xOt

HD: Gọi tọa độ ba điểm A, B, C lần lượt là

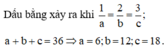
Vậy độ dài ba cạnh OA, OB, OC lần lượt theo thứ tự lập thành cấp số cộng. Chọn C.

Đáp án A
Dễ dàng suy ra:
A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c , a , b , c > 0
vì d M ; O B C = d M ; O y z = x M = 1 , tương tự ta có được M 1 ; 2 ; 3
M ∈ A B C ⇔ 1 a + 2 b + 3 c ≥ 3 1.2.3 a . b . c 3 ⇔ a b c 6 = V O . A B C ≥ 27
Dấu bằng xảy ra khi:
1 a = 2 b = 3 c = 1 3 ⇒ a = 3 ; b = 6 ; c = 9 ⇒ a + b + c = 18