Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số tiền của 3 người thợ lần lượt là x,y,z
Vì số tiền thưởng và năng suất lao động là 2 đại lượng tỉ lệ thuận nên
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{7}\)
Theo tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{z}{7}=\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z-x}{7-3}=\dfrac{200000}{4}=50000\)
\(\Rightarrow x=50000.3=150000\)
\(y=50000.5=250000\)
\(z=50000.7=350000\)
Số tiền thưởng của 3 người thợ lần lượt là 150000,250000,350000 ( đồng )

a) Gọi số tiền thưởng của ba người lần lượt là a,b,c(triệu đồng)
Theo điều kiện của bài ta có : \(a:b:c=3:5:7\)hoặc \(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\)và a + b = 5,6
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b}{3+5}=\frac{5,6}{8}=0,7\)
=> \(\hept{\begin{cases}\frac{a}{3}=0,7\\\frac{b}{5}=0,7\\\frac{c}{7}=0,7\end{cases}}\Rightarrow\hept{\begin{cases}a=2,1\\b=3,5\\c=4,9\end{cases}}\)
=> \(a+b+c=2,1+3,5+4,9=10,5\)
Vậy tổng số tiền của ba người được thưởng là 10,5 triệu đồng
Còn câu b bạn tự làm đi nhé

Gọi x,y,z là số tiền thưởng của ba công nhân lần lượt (x,y,z > 0)
Gỉa sử x,y,z tỉ lệ thuận với 3;4;7 ta có: x 3 = y 5 = z 7 và x+ y = 5,6
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
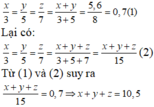
Tổng số tiền thưởng của ba người là 10,5 triệu
Đáp án cần chọn là C

Gọi tiền thưởng của 3 người lần lượt là a,b,c (triệu)(a,b,c>0).
Tổng số tiền thưởng của ng1 và ng2 là 5,6 triệu đồng nên a+b=5,6
Số tiền thưởng tỉ lệ thuận với năng suất lao động nên: a3=b5=c7=a+b3+5=5,68=0,7.
⇒a=0,7.3=2,1(tr);b=0,7.5=3,5(tr);c=0,7.7=4,9(tr).
Do đó tổng tiền thưởng của 3ng là:2,1+3,5+4,9=10,5(tr).
Nếu đúng thì tích mình nha bạn

Giải:
Gọi số tiền thưởng của 3 người lần lượt là a, b, c ( a,b,c thuộc N* )
Ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\) và \(a+b=5600000\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b}{3+5}=\frac{5600000}{8}=700000\)
+) \(\frac{a}{3}=700000\Rightarrow a=2100000\)
+) \(\frac{b}{5}=700000\Rightarrow b=3500000\)
+) \(\frac{c}{7}=700000\Rightarrow c=4900000\)
Vậy người thứ nhất được 2100000 đồng ( 2.1 triệu )
người thứ 2 được 3500000 đồng ( 3.5 triệu )
người thứ 3 được 4900000 đồng ( 4.9 triệu )
Gọi tiền thưởng của 3 người lần lượt là a,b,c (triệu)(a,b,c>0).
Tổng số tiền thưởng của người 1 và người 2 là 5,6 triệu đồng nên a+b=5,6
Số tiền thưởng tỉ lệ thuận với năng suất lao động nên:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b}{3+5}=\frac{5,6}{8}=0,7\)
\(\Rightarrow a=0,7.3=2,1\) ;\(b=0,7.5=3.5\) ;\(c=0,7.7\) =4,9
Do đó tổng tiền thưởng của 3ng là:2,1+3,5+4,9=10,5(tr)2,1+3,5+4,9=10,5(tr).

gọi x;y;z lần lượt là số tiền thưởng của ba người
theo đề ta có :
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}\)và z-x=4
áp dụng tính chất của dãy tỉ số bằng nhau ta có;
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{z-x}{7-3}=\frac{4}{4}=1\)
suy ra \(\frac{x}{3}=1\Rightarrow x=3\)
\(\frac{y}{5}=1\Rightarrow y=5\)
\(\frac{z}{7}=1\Rightarrow z=7\)
vậy số tiền thưởng của 3 người lần lượt là 3 triệu ;5 triệu ; 7 triệu
=>tổng số tiền của 3 người là 15 triệu

Giải:
Gọi số tiền thưởng của 3 người lần lượt là a, b, c \(\left(a,b,c>0\right)\)
Ta có: \(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}\) và \(a+b=7,2\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+b}{3+5}=\frac{7,2}{8}=0,9\)
+) \(\frac{a}{3}=0,9\Rightarrow a=2,7\)
+) \(\frac{b}{5}=0,9\Rightarrow b=4,5\)
+) \(\frac{c}{7}=0,9\Rightarrow c=6,3\)
\(\Rightarrow a+b+c=13,5\)
Vậy tổng số tiền thưởng của 3 người là 13,5 triệu đồng
Mk rảnh nên gõ trong Wold nên hơi lâu xíu , thông cảm!