Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số máy mỗi đội lần lượt có là: a,b,c ( máy ) ( a,c,b \(\in\)N* , b > 1 )
Theo bài ra , ta có : b - c = 1
Vì số máy tỉ lệ nghịch với số ngày nên: 3a = 5b= 6c
\(\Rightarrow\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{5}}=\frac{c}{\frac{1}{6}}=\frac{b-c}{\frac{1}{5}-\frac{1}{6}}=\frac{1}{\frac{1}{30}}=30\)
\(\Rightarrow\hept{\begin{cases}a=30.\frac{1}{3}=10\\b=30.\frac{1}{5}=6\\c=30.\frac{1}{6}=5\end{cases}}\)
Vậy sô máy của 3 đội lần lượt là 10 ; 6 ; 5 máy.
gọi số máy cày của 3 đội lần lướt là a , b , c.
theo bài ra,ta có : b-c=1
vì số máy cày tỉ lệ nghịch với số ngày hoàn thành công việc nên ,ta có:
a/1/3=b/1/5=c/1/6
áp dụng tính chất dãy tỉ số bằng nhau , ta có
a/1/3=b/1/5=c/1/6=b-c/1/5-1/6=1/1/30
=> a=30 nhân\(\frac{1}{3}\)= 10
b=30 nhân \(\frac{1}{5}\)=6
c=30 nhân \(\frac{1}{6}\)=5
vậy đọi 1 có 10 máy
đội 2 có 6 máy
đọi 3 có 5 máy

Bạn làm như bình thường nhé. còn kkhi ADTCDTSBN thì bạn nhân cả tử và mẫu của c/3 với 2 nhé( mình tạm gọi số máy đội 3 là c nhé)
Gọi a,b,c là số máy cày của mỗi đội (a,b,c thuộc N*)
Vì số máy và số ngày tỉ lệ nghịch với nhau nên ta có: a,b,c TLN với 3,5,6
=> a3 = b5 = c6
=> a/1/3=b/1/5=c/1/6 và b-c = 1
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
a/1/3=b/1/5=c/1/6=b−c/15−16=1/1/30=30
a/1/3=30 => a = 10
b/1/5=30 => b = 6
c/1/6=30 => c = 5
Vậy số máy của mỗi đội lần lượt là 10 máy, 6 máy, 5 máy

Gọi x (máy), y (máy), z (máy) lần lượt là số máy cày của các đội 1, 2, 3 (điều kiện x, y, z ∈ N*)
Vì diện tích các cánh đồng là như nhau nên số máy cày và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch, suy ra 3x = 5y = 6z.
Đội thứ hai nhiều hơn đội thứ ba 1 máy nên y – z = 1.
Từ 3x = 5y = 6z, suy ra
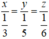
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
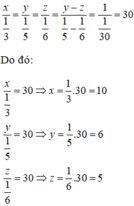
Vậy đội 1 có 10 máy cày, đội hai có 6 máy và đội 3 có 5 máy

Gọi số máy của đội 1;2;3 lần lượt là a,b,c
Theo đề, ta có: 3a=5b=6c và a-c=5
=>a/10=b/6=c/5 và a-c=5
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{5}=\dfrac{a-c}{10-5}=1\)
=>a=10; b=6; c=5

Gọi số máy cày của 3 đọi lần lượt là: a;b;c (máy)
Với cùng 1 diện tích đất thì số máy cày và thời gian làm xong việc là 2 ĐLTLN; ta có:
a3=b5=c6=>a/(1/3)=b/(1/5)=c/(1/6) và b-c=1
ttcdtsbn; ta có:
a/(1/3)=b/(1/5)=c/(1/6)=(b-c)/(1/5-1/6)=1/(1/30)=30
Khi đó: a=10; b=6; c=5
Vậy số máy của 3 đội lần lượt là 10;6;5
Gọi số máy cày của 3 đọi lần lượt là: a;b;c (máy)
Với cùng 1 diện tích đất thì số máy cày và thời gian làm xong việc là 2 ĐLTLN; ta có:
a3=b5=c6=>a/(1/3)=b/(1/5)=c/(1/6) và b-c=1
ttcdtsbn; ta có:
a/(1/3)=b/(1/5)=c/(1/6)=(b-c)/(1/5-1/6)=1/(1/30)=30
Khi đó: a=10; b=6; c=5
Vậy số máy của 3 đội lần lượt là 10;6;5

Giải:
Gọi số máy cày của mỗi đội lần lượt là a, b, c.
Vì số máy cày và số ngày làm việc tỉ lệ nghịch với nhau nên ta có:
\(a.3=b.5=c.6\) và \(b-c=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{5}=\dfrac{b}{3}\\\dfrac{b}{6}=\dfrac{c}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{10}=\dfrac{b}{6}\\\dfrac{b}{6}=\dfrac{c}{5}\end{matrix}\right.\Leftrightarrow\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{5}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\Leftrightarrow\dfrac{a}{10}=\dfrac{b}{6}=\dfrac{c}{5}=\dfrac{b-c}{6-5}=\dfrac{1}{1}=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{a}{10}=1\\\dfrac{b}{6}=1\\\dfrac{c}{5}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=10\\b=6\\c=5\end{matrix}\right.\)
Vậy số máy cày của mỗi đội lần lượt là 10 máy, 6 máy và 5 máy.
Giải :
Gọi a,b,c là số máy cày lần lượt tỉ lệ với các số 3,5,6 và b - c = 2
Vì số máy cày và số ngày làm việc là hai đại lượng tỉ lệ nghịch nên ta có :
a/1/3 = b/1/5 = c/1/6 = b/1/5 - c/1/6 = 2/1/30 = 60
Do đó :
a/1/3 = 60 => a = 60.1/3 = 20
b/1/5 = 60 => b = 60.1/5 = 12
c/1/6 = 60 => c = 60.1/6 =10
Vậy số máy cày của ba đội lần lượt là : 20 ; 12 ; 10

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{\dfrac{1}{3}}=\dfrac{b}{\dfrac{1}{5}}=\dfrac{c}{\dfrac{1}{6}}=\dfrac{b-c}{\dfrac{1}{5}-\dfrac{1}{6}}=30\)
Do đó: a=10; b=6; c=5
Gọi số máy cày của ba đội lần lượt là a,b,c (a,b,c nguyên dương)
Theo bài ra ta có: b - c = 1
Vì số máy cày và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch nên ta có:
3.a = 5.b =6.c hay
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
=>
Vậy số máy cày của ba đội lần lượt là: 10; 6; 5.