K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 3 2016
bai 1
1 thay k=0 vao pt ta co 4x^2-25+0^2+4*0*x=0
<=>(2x)^2-5^2=0
<=>(2x+5)*(2x-5)=0
<=>2x+5=0 hoăc 2x-5 =0 tiếp tục giải ý 2 tương tự
12 tháng 6 2019
a) \(x\left(2x+1\right)-x^2\left(x+2\right)+\left(x^3-x+3\right)\)
\(=2x^2+x-x^3-2x^2+x^3-x+3\)
\(=3\)
Vậy bt trên ko phụ vào biến x
b) \(x\left(3x^2-x+5\right)-\left(2x^3+3x-16\right)-x\left(x^2-x+2\right)\)
\(=3x^3-x^2+5x-2x^3-3x+16-x^3+x^2-2x\)
\(=16\)
Vậy bt trên ko phụ vào biến x
20 tháng 12 2017
[x² - 2mx - 4(m²+1)].[x² - 4x - 2m(m²+1)] = 0 (1)
pt (1) tương đương với tuyển hai pt:
[x² - 2mx - 4(m²+1) = 0 (*)
[x² - 4x - 2m(m²+1) = 0 (**)
- - -
∆' (*) = m² + 4(m²+1) = 5m² + 1 > 0 với mọi m => (*) luôn có hai nghiệm phân biệt
∆' (**) = 4 + 2m(m²+1) = 2(m+1)(m² - m + 2)
Thấy m² - m + 2 = (m - 1/2)² + 7/4 > 0 với mọi m
=> (**) có nghiệm khi và chỉ khi ∆'(**) ≥ 0 <=> m+1 ≥ 0 <=> m ≥ -1
- - -
Trước tiên ta xét trường hợp (*) và (**) có nghiệm chung khi đó ta có hệ:
{x² - 2mx - 4(m²+1) = 0 (1*)
{x² - 4x - 2m(m²+1) = 0 (2*)
trừ vế ta được: (2m-4)x - 2m(m²+1) + 4(m²+1) = 0
<=> (m-2)x - (m-2)(m²+1) = 0
nếu m = 2, khi đó cả hai pt (1*) và (2*) thành x² - 4x - 20 = 0
chứng tỏ (*) và (**) trùng nhau nên (1) chỉ có 2 nghiệm, không thỏa yêu cầu
Vậy m # 2, từ trên => x = m²+1 ; thay vào (1*) ta có: (m²+1)² - 2m(m²+1) - 4(m²+1) = 0
<=> m²+1 - 2m - 4 = 0 (do m²+1 > 0 ) <=> m² - 2m - 3 = 0 <=> m = -1 hoặc m = 3
- - - các bước chhuẩn bị đã xong, giờ thì bắn thôi - - -
(1) có 3 nghiệm phân biệt khi và chỉ khi (**) có nghiệm kép khác với hai nghiệm của (*), hoặc (**) có hai nghiệm pb trong đó có một nghiệm trùng với một nghiệm của (*)
* TH1: (**) có nghiệm kép khi và chỉ khi m = -1 , nhưng khi đó
(*) và (**) lại có nghiệm chung tức nghkép này đã bị trùng với nghiệm của (*)
=> (1) có 2 nghiệm - không thỏa
* TH2: (**) có hai nghiệm pbiệt, trong đó 1 nghiệm trùng với nghiệm của (*)
=> ta phải có: m > -1 và m = -1 hoặc m = 3 => m = 3
**Đảo lại khi m = 3: (*) có nghiệm là x = -4 ; x = 10; (**) có
nghiệm là: x = -6 ; x = 10
=> (1) có đúng 3 nghiệm là x = -6; x = -4 ; x = 10
Tóm lại: ta chọn được m = 3
Tk cho mk, mk tk lại
19 tháng 3 2020
Bài 1 : Chứng minh phương trình vô nghiệm :
a, Ta có : \(x+2=x+5\)
=> \(x+2-x-5=0\)
=> \(-3=0\left(VL\right)\)
Vậy phương trình vô nghiệm .
b, Ta có : \(x^2-x+1=0\)
=> \(\left(x-\frac{1}{2}\right)^2+\frac{3}{4}=0\) ( Vô lý )
Vậy phương trình vô nghiệm .
24 tháng 5 2017
a) \(a^3+b^3+3ab\)
\(=\left(a+b\right)\left(a^2-ab+b^2\right)+3ab\)
\(=a^2-ab+b^2+3ab\)
\(=a^2+2ab+b^2=\left(a+b\right)^2\)
\(=1^2=1\)
b) \(x^3+y^3-3xy\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)-3xy\)
\(=-\left(x^2+2xy+y^2\right)=-1^2=-1\)
c) A:Điều kiện xác định của P là \(x\ne-2\)
B: bạn tự làm nha......................
30 tháng 5 2017
cảm ơn nhưng lúc sau bik làm hết rồi chỉ còn mỗi tìm điều kiện thôi!
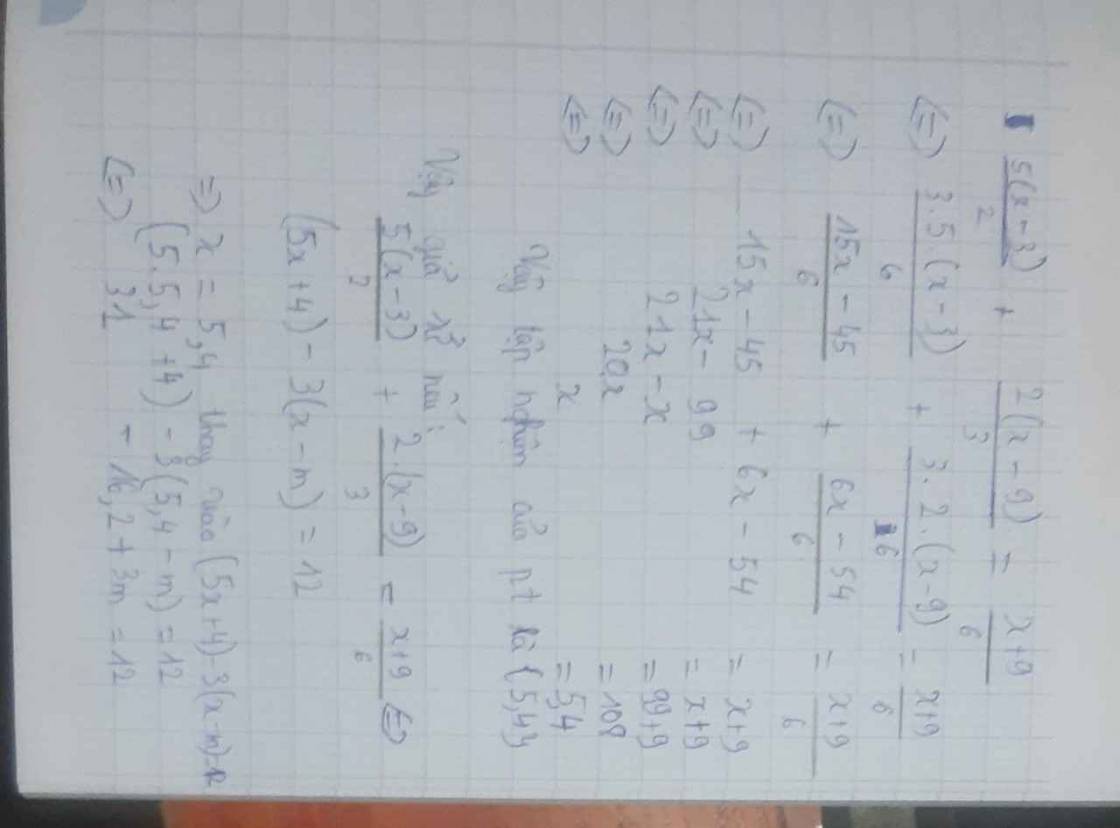
\(ĐKXĐ:x\ne0,x\ne3\)
đkxđ: x ≠ 0 , x ≠ 3