
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Giả sử f(x) có nghiệm nguyên
=>x3-x=5
=>x(x2-1)=5
Nếu x chẵn thì x(x2-1) chẵn, loại
Nếu x lẻ thì x2 lẻ =>x2-1 chẵn => x(x2-1) chẵn, loại
Vậy f(x) ko có nghiệm nguyên

\(\left|x+\dfrac{1}{7}\right|-\dfrac{2}{3}=0\)
\(\Rightarrow\left|x+\dfrac{1}{7}\right|=0+\dfrac{2}{3}\\ \Rightarrow\left|x+\dfrac{1}{7}\right|=\dfrac{2}{3}\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{1}{7}=\dfrac{2}{3}\\x+\dfrac{1}{7}=-\dfrac{2}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}-\dfrac{1}{7}\\x=-\dfrac{2}{3}-\dfrac{1}{7}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{11}{21}\\x=-\dfrac{17}{21}\end{matrix}\right.\)

Ta có \(x1-\frac{1}{9}=x2-\frac{2}{8}=...=x9-\frac{9}{1}\)
\(=\frac{x1-1}{9}=\frac{x2-2}{8}=\frac{x3-3}{7}=...=\frac{x9-9}{1}\)
= \(\frac{x1-1+x2-2+x3-3+...+x9-9}{9+8+7+...+1}\)
\(=\frac{\left(x1+x2+x3+...+x9\right)-\left(1+2+3+...+9\right)}{9+8+7+....+1}\)
=\(\frac{90-45}{45}=\frac{45}{45}=1\)
=> \(\hept{\begin{cases}\begin{cases}x1=10\\x2=10\end{cases}\\.....\\x9=10\end{cases}}\)

Bài này có rất nhiều bạn chịu khó tìm là thấy
http://olm.vn/hoi-dap/question/602922.html
Đề bài đúng với mọi n > 0 không nhất thiết phải nguyên hoặc = 2011.
Cách so sanh thường là xét hiệu rồi biện luận >0 hoặc <0.

Bài 3:
theo đề bài ta có:
\(\left\{{}\begin{matrix}2a-3b=0\\5b-7c=0\\3a-7b+5c=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=42\\b=28\\c=20\end{matrix}\right.\)
Bài 4:
Đặt \(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{6}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k\\y=5k\\z=6k\end{matrix}\right.\)
Ta có: \(x^2-2y^2+z^2=18\)
\(\Leftrightarrow16k^2-50k^2+36k^2=18\)
\(\Leftrightarrow k^2=9\)
Trường hợp 1: k=3
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=4\cdot3=12\\y=5k=5\cdot3=15\\z=6k=6\cdot3=18\end{matrix}\right.\)
Trường hợp 2: k=-3
\(\Leftrightarrow\left\{{}\begin{matrix}x=4k=-3\cdot4=-12\\y=5k=-3\cdot5=-15\\z=6k=-3\cdot6=-18\end{matrix}\right.\)
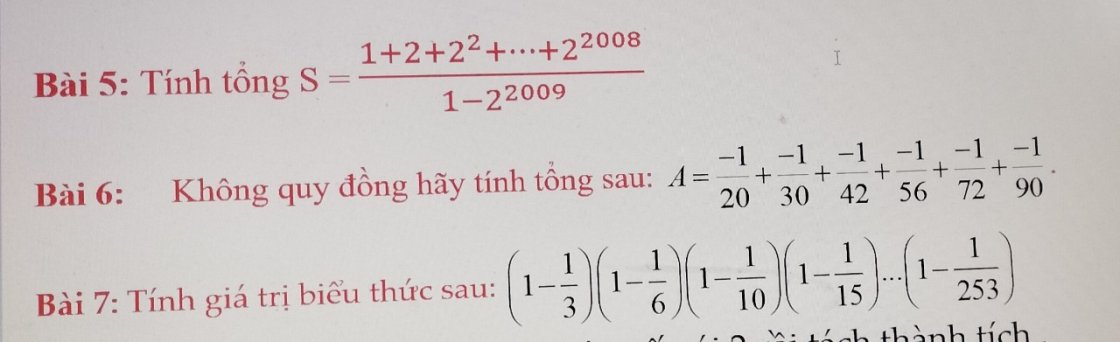 các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm
các anh chị giải giúp em bài này đc ko ạ em đang cần gấp nắm giúp em câu này nữa ạ, làm phiền mấy anh chị rồi ạ, xl :)
giúp em câu này nữa ạ, làm phiền mấy anh chị rồi ạ, xl :)
bài nào bạn?
Bài nào vậy bạn? Mik ko thấy