
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1. Ta sẽ chứng minh dựa trên các kết quả quen thuộc sau về tâm I của đường tròn nội tiếp tam giác:
\(a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}=\overrightarrow{0}\)
Và: \(a.IA^2+b.IB^2+c.IC^2=abc\)
Đẳng thức thứ nhất chỉ cần dựng hình bình hành AMIN, sau đó sử dụng định lý phân giác các góc B và C.
Đẳng thức thứ hai ta chỉ cần lấy 1 điểm P nào đó đối xứng I qua AC, gọi D, E, F là tiếp điểm của (I) với BC, AC, AB, sau đó sử dụng tỉ lệ diện tích:
\(\dfrac{S_{AEIF}}{S_{ABC}}=\dfrac{S_{AIK}}{S_{ABC}}=\dfrac{AI.AK}{AB.AC}=\dfrac{IA^2}{bc}\)
Tương tự và cộng lại ...
Từ đó:
\(a.MA^2+b.MB^2+c.MC^2=a.\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+b\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+c.\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2\)
\(=\left(a+b+c\right)MI^2+a.IA^2+b.IB^2+c.IC^2+2\overrightarrow{MI}\left(a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}\right)\)
\(=\left(a+b+c\right)MI^2+abc\ge abc\)
Dấu "=" xảy ra khi \(MI=0\) hay M là tâm đường tròn nội tiếp
2. Do a;b;c là độ dài 3 cạnh của tam giác, thực hiện phép thế Ravi:
Đặt \(\left(a;b;c\right)=\left(x+y;y+z;z+x\right)\)
BĐT cần chứng minh tương đương:
\(4\left(x+y+z\right)\left(x^2+y^2+z^2+xy+yz+zx\right)\ge3\left(x^3+y^3+z^3+3xyz+xy\left(x+y\right)+yz\left(y+z\right)+zx\left(z+x\right)\right)\)
\(\Leftrightarrow x^3+y^3+z^3+3xyz\ge xy\left(x+y\right)+yz\left(y+z\right)+zx\left(z+x\right)\)
Đây là BĐT Schur bậc 3

\(\left(a^3+b^3\right)\left(a+b\right)=ab\left(1-a\right)\left(1-b\right)\)
\(\Leftrightarrow\left(1-a\right)\left(1-b\right)=\left(\dfrac{a^2}{b}+\dfrac{b^2}{a}\right)\left(a+b\right)\ge\left(a+b\right)^2\ge4ab\)
\(\Rightarrow1+ab-4ab\ge a+b\ge2\sqrt{ab}\)
\(\Rightarrow3ab+2\sqrt{ab}-1\le0\)
\(\Leftrightarrow\left(\sqrt{ab}+1\right)\left(3\sqrt{ab}-1\right)\le0\)
\(\Leftrightarrow ab\le\dfrac{1}{9}\)

a) Từ giả thiết => a1+a2+a3<3a3
a4+a5+a6<3a6
a7+a8+a8<3a9
=>\(a_1+a_2+...+a_9< 3\left(a_3+a_6+a_9\right)\Leftrightarrow\dfrac{a_1+a_2+...+a_9}{a_3+a_6+a_9}< 3\left(ĐPCM\right)\)
b)Câu này phải là \(\ge\) chứ không phải > nha bạn:
Ta có:
(a-b)2\(\ge\)0 với mọi ab
<=>a2+b2\(\ge\)2ab(1) với mọi ab
Dấu "=" xảy ra khi và chỉ khi (a-b)2=0 <=> a=b
Chứng minh tương tự ta được a2+1\(\ge\)2a(2) ; b2+1\(\ge\)2b(3)
Dấu "=" xảy ra khi và chỉ khi a=1 ; b=1
Cộng vế với vế của (1);(2) và (3):
2(a2+b2+1)\(\ge\)2(ab+a+b)
<=> a2+b2+1\(\ge\)ab+a+b
Dấu bằng xảy ra khi và chỉ khi \(\left\{{}\begin{matrix}a=b\\b=1\\a=1\end{matrix}\right.\Leftrightarrow}a=b=1\)

Pt hoành độ giao điểm (d) và (P):
\(x^2-8x=x-m\Leftrightarrow x^2-9x+m=0\)
\(\Delta=81-4m\ge0\Rightarrow m\le\dfrac{81}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}a+b=9\\ab=m\end{matrix}\right.\)
\(a^3+b^3=675\Leftrightarrow\left(a+b\right)^3-3ab\left(a+b\right)=675\)
\(\Leftrightarrow9^3-27m=675\)
\(\Rightarrow m=2\)
Pt hoành độ giao điểm (d) và (P):
x\(^2\)
−8x=x−m⇔x\(^2\)
−9x+m=0
Δ=81−4m≥0⇒m≤\(\dfrac{81}{4}\)
Theo hệ thức Viet: \left\{{}\begin{matrix}a+b=9\\ab=m\end{matrix}\right.\(\left\{{}\begin{matrix}a+b=9\\ab=m\end{matrix}\right.\)
a
\(^3\)+b
\(^3\)=675⇔(a+b)\(^3\)
−3ab(a+b)=675
\Leftrightarrow9^3-27m=675⇔9
\(^3\)−27m=675
\Rightarrow m=2⇒m=2

Áp dụng bđt Cô- si với các số a,b,c>0:
\(a^3+1+1\ge3a,b^3+1+1\ge3b,c^3+1+1\ge3c\)
\(\Rightarrow a^3+b^3+c^3+6\ge3a+3b+3c\)
\(\Rightarrow a^3+b^3+c^3\ge a+b+c+2\left(a+b+c\right)-6\ge a+b+c+2\cdot3\sqrt[3]{abc}-6=a+b+c+6-6=a+b+c\)
Vậy...
đề là chứng minh bất đẳng thức
bạn nào giải được giúp mình với, mình cảm ơn !

\(F=\left(a+b\right)^3-3ab\left(a+b\right)+ab=1-2ab\)
Ta có F đạt giá trị nhỏ nhất khi -2ab đạt giá trị nhỏ nhất.
Vì \(a+b=1\) có tổng không đổi nên \(-2ab\) đạt giá trị
nhỏ nhất khi ab đạt giá trị lớn nhất <=> a = b = 1/2
Thay a = b = 1/2 vào F tính được min F.
Ta có : F = (a+b)(a2 –ab+b2) +ab
Thay a+ b =1 vào F ta được F = a2 – ab +b2 + ab
F = a2 +b2 F = (a+b)2 – 2ab
F = 1 – 2ab Do a+b =1 ⇔ a = 1-b
thay vào F ta có : F = 1- 2(1-b)b F = 1 -2b+2b2 F = 2(b2 – b+41) + 21 F = 2(b -21)2 +21≥21
Với mọi b Dấu “ = ” xảy ra khi : b -21 = 0 ⇔ b =21 và a =21 Vậy Min F = 21 Khi a =b = 21

1.
Theo nguyên lý Dirichlet, trong 3 số a;b;c luôn có 2 số cùng phía so với \(\dfrac{2}{3}\), không mất tính tổng quát, giả sử đó là b và c
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\ge0\)
Mặt khác \(0\le a\le1\Rightarrow1-a\ge0\)
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\left(1-a\right)\ge0\)
\(\Leftrightarrow-abc\ge\dfrac{4a}{9}+\dfrac{2b}{3}+\dfrac{2c}{3}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}\)
\(\Leftrightarrow-abc\ge-\dfrac{2a}{9}+\dfrac{2}{3}\left(a+b+c\right)-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}=-\dfrac{2a}{9}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc+\dfrac{8}{9}\)
\(\Leftrightarrow-2abc\ge-\dfrac{4a}{9}-\dfrac{4ab}{3}-\dfrac{4ac}{3}-2bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{ab}{3}-\dfrac{ac}{3}-bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(b+c\right)-bc+\dfrac{16}{9}\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(2-a\right)-\dfrac{\left(b+c\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}+\dfrac{a^2}{3}-\dfrac{2a}{3}-\dfrac{\left(2-a\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge\dfrac{a^2}{12}-\dfrac{a}{9}+\dfrac{7}{9}=\dfrac{1}{12}\left(a-\dfrac{2}{3}\right)^2+\dfrac{20}{27}\ge\dfrac{20}{27}\)
\(\Rightarrow ab+bc+ca\ge2abc+\dfrac{20}{27}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{2}{3}\)

BĐT \(\Leftrightarrow a^3-b^3+a^2b-ab^2\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a^2+ab+b^2\right)+ab\left(a-b\right)\ge0\)
\(\Leftrightarrow\left(a-b\right)\left(a+b\right)^2\ge0\) (luôn đúng do \(a\geq b\)).
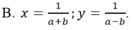
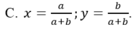
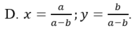
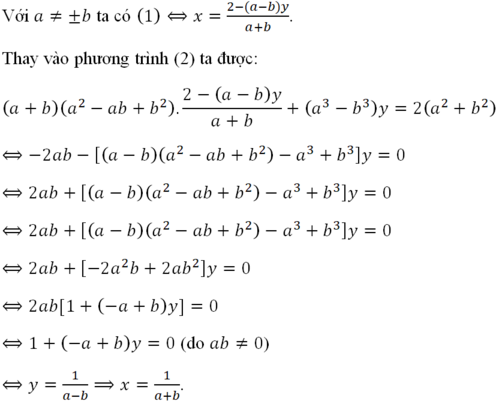
Lời giải:
Lần sau bạn lưu ý, gõ đầy đủ đề, gõ đúng công thức toán để được hỗ trợ tốt hơn.
Bổ sung: $a,b>0$
Xét hiệu:
$a^3+b^3-ab(a+b)=(a+b)(a-b)^2\geq 0$ với mọi $a,b>0$
$\Rightarrow a^3+b^3\geq ab(a+b)$
$\Rightarrow 3(a^3+b^3)\geq 3ab(a+b)$
$\Rightarrow 4(a^3+b^3)\geq a^3+b^3+3ab(a+b)=(a+b)^3$
$\Rightarrow \frac{a^3+b^3}{2}\geq \frac{(a+b)^3}{8}=\left(\frac{a+b}{2}\right)^3$ (đpcm)
Dấu "=" xảy ra khi $a=b$