ET
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DM
0
PT
11 tháng 8 2017
\(\dfrac{21}{47}+\dfrac{9}{45}+\dfrac{26}{47}+\dfrac{4}{5}\)
\(=\left(\dfrac{21}{47}+\dfrac{26}{47}\right)+\left(\dfrac{9}{45}+\dfrac{4}{5}\right)\)
\(=1+1\)
\(=2\)
D
4
A
22 tháng 6 2018
\(-\left(32+47\right)+96-168+47\)
\(=-32+\left(-47\right)+96-168+47\)
\(=\left(-32-168\right)+\left(-47+47\right)+96\)
\(=-200+0+96\)
\(=-104\)
22 tháng 6 2018
\(-\left(32+47\right)+96-168+47\)
\(=-32+\left(-47\right)+96-168+47\)
\(=\left(-47+47\right)+\left(-32-168\right)+96\)
\(=0-200+96\)
\(=-104\)
TV
6 tháng 6 2017
Trần Khánh Hiền
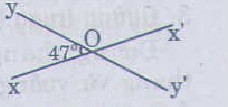
Giả sử hai đường thẳng xx' và yy' cắt nhau tại O và ˆxOy=47∘xOy^=47∘ (hình vẽ bên). Suy ra ˆx′Oy′=ˆxOy=47∘x′Oy′^=xOy^=47∘ (hai góc đối đỉnh).
ˆxOy′=180∘−ˆxOy=180∘−47∘=133∘xOy′^=180∘−xOy^=180∘−47∘=133∘ (do ˆx′Oyx′Oy^ và ˆxOy′xOy′^ kề bù)
Và ˆx′Oy=ˆxOy′=133∘x′Oy^=xOy′^=133∘ (hai góc đối đỉnh).
6 tháng 6 2017
Giả sử hai đường thẳng xx' và yy' cắt nhau tại O và ˆxOy=47∘xOy^=47∘ (hình vẽ bên). Suy ra ˆx′Oy′=ˆxOy=47∘x′Oy′^=xOy^=47∘ (hai góc đối đỉnh).
ˆxOy′=180∘−ˆxOy=180∘−47∘=133∘xOy′^=180∘−xOy^=180∘−47∘=133∘ (do ˆx′Oyx′Oy^ và ˆxOy′xOy′^ kề bù)
Và ˆx′Oy=ˆxOy′=133∘x′Oy^=xOy′^=133∘ (hai góc đối đỉnh).
\(42\cdot53+47\cdot156-47\cdot114\)
\(=42\cdot53+47\left(156-114\right)\)
\(=42\cdot53+47\cdot42\)
\(=42\left(53+47\right)=42\cdot100=4200\)
\(42.53+47.156-47.114\)
\(=42.53+47.\left(156-114\right)\)
\(=42.53+47.42\)
\(=42.\left(47+53\right)\)
\(=42.100\)
\(=4200\)