Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) \(W_đ=W_t\Rightarrow W=W_đ+W_t=2W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=2.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{A}{\sqrt 2}\)
Như vậy, trong 1 chu kì có 4 lần động năng bằng thế năng được biểu diễn bằng véc tơ quay như sau.
x A -A O M N P Q
Đó là các vị trí ứng với véc tơ quay đi qua M, N, P, Q
Như vậy, thời gian giữa 2 lần liên tiếp động năng bằng thế năng là 1/4T
\(\Rightarrow \dfrac{T}{4}=0,2\Rightarrow T = 0,8s\)
\(W_đ=nW_t\)
\(\Rightarrow W = W_đ+W_t=nW_t+W_t=(n+1)W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=(n+1).\dfrac{1}{2}kx^2\)
\(\Rightarrow \dfrac{A}{x}=\pm\sqrt{n+1}\)
\(\Rightarrow \dfrac{\omega^2. A}{-\omega^2.x}=\pm\sqrt{n+1}\)
\(\Rightarrow \dfrac{a_{max}}{a}=\pm\sqrt{n+1}\)

Gọi A là biên độ giao động ta có : kA = 10 N; kA2/2 = 1J => A = 0,2 m = 20 cm
Khoảng thời gian ngắn nhất giữa 2 lần liên tiếp Q chịu tác dụng lực kéo của lò xo có độ lớn \(5\sqrt{3}\)
=> Chu kì giao động của vật T = 0,6s
Quãng đường ngắn nhất đi được là trong 0,4s = \(\frac{2T}{3}\) là s = 3A = 60 cm
Vậy B đúng

Để tính giá trị của t, ta sử dụng công thức:
t = φ / ω
Trong đó:
t là thời gian tính từ lúc con lắc bắt đầu dao động.φ là pha ban đầu của dao động.ω là tần số góc của dao động.Theo đề bài, tần số góc ω = 5π rad/s và pha ban đầu φ = -π/3 rad. Thay vào công thức trên, ta có:
t = (-π/3) / (5π) = -1/15 s
Tuy nhiên, thời gian không thể có giá trị âm, vì vậy giá trị của t là 1/15 s.

Đáp án C
Phương pháp: Sử dụng định luật bảo toàn cơ năng W = Wđ + Wt
Cách giải:
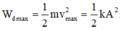
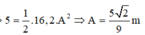
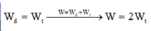
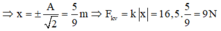

Đáp án C
Động năng cực đại = thế năng cực đại ⇒ 1 2 k A 2 = 5 ⇒ A = 5 2 9
Động năng = thế năng tại A 2 2 = 5 9 c m
F = kx = 16,2.5/9 = 9 N

Tại thời điểm ban đầu động năng cực đại nên vận tốc cực đại, tức là ban đầu vật đang ở vị trí cân bằng.
Khi động năng \(W_đ=\frac {W_{đmax}} {2}=\frac W 2\)(W là cơ năng của vật, tại vị trí cân bằng động năng bằng cơ năng)
Bảo toàn cơ năng W=Wđ+Wt
\(W_t=\frac W 2<=>\frac 1 2 kx^2=\frac 1 4 kA^2 <=>x=\frac A 2\).
y x x/2 λ A
Để đi từ vị trí cân bằng đến vị trí \(\frac A 2\) thì thời gian ngắn nhất là t=\(\frac {λΔt} {360} =\frac {60Δt} {360}=\frac {Δt} 6 \)
<=> Chọn câu C.