
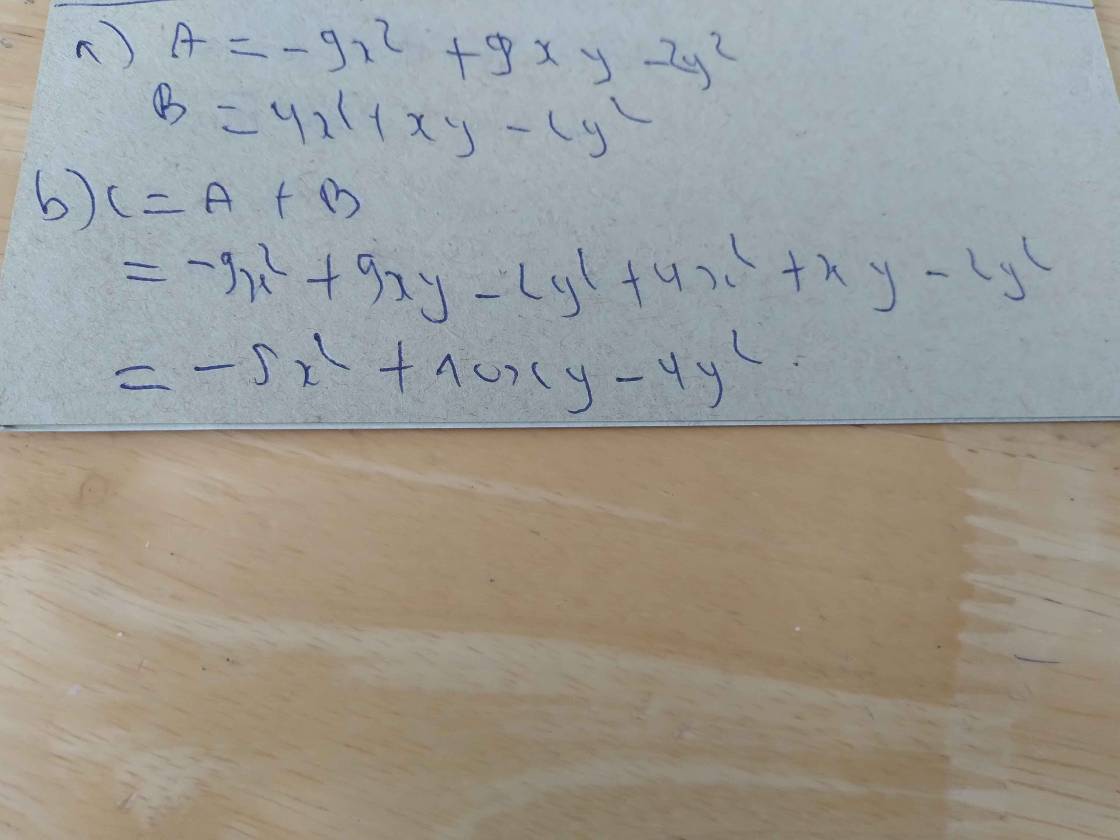
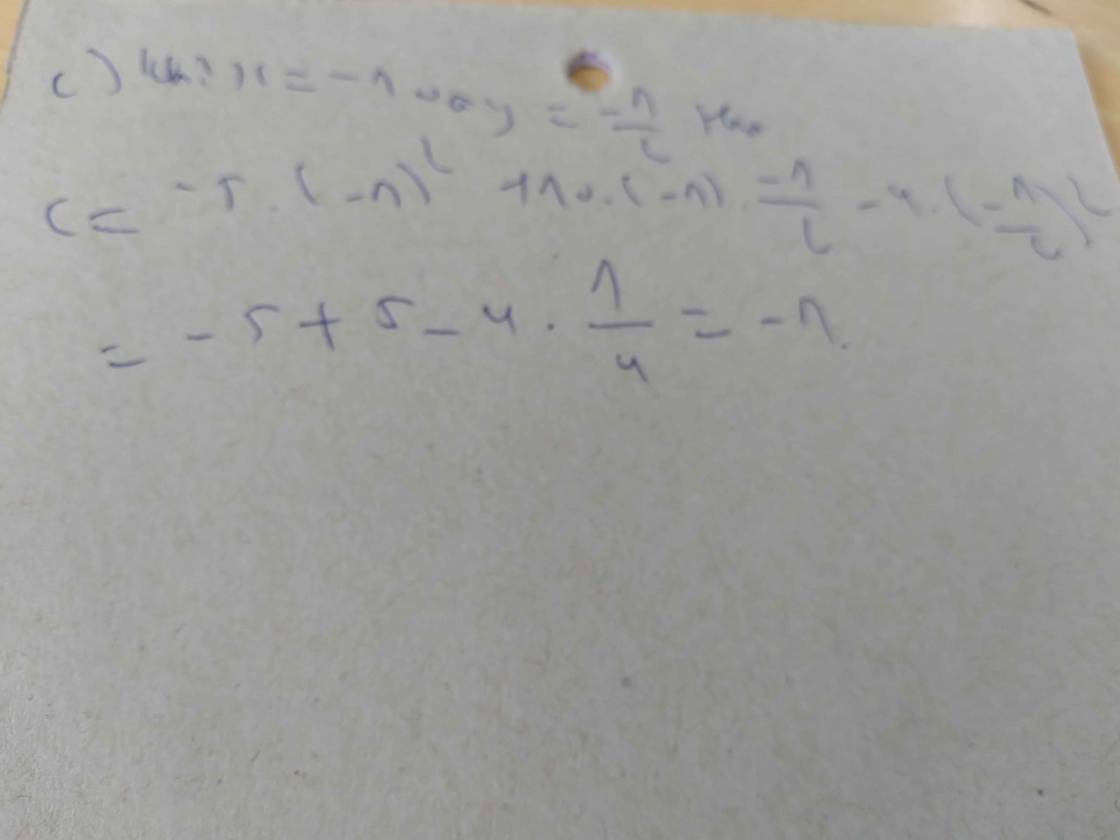
A= -7x2 - 3y2 + 9...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

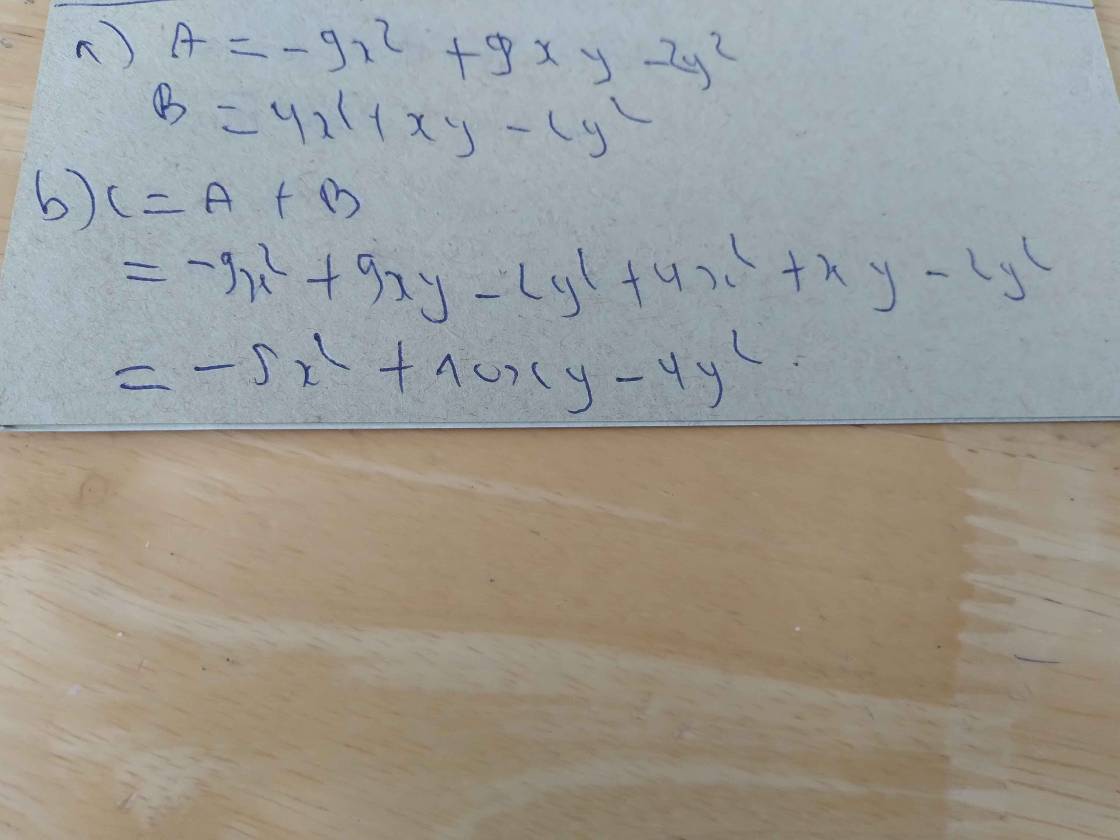
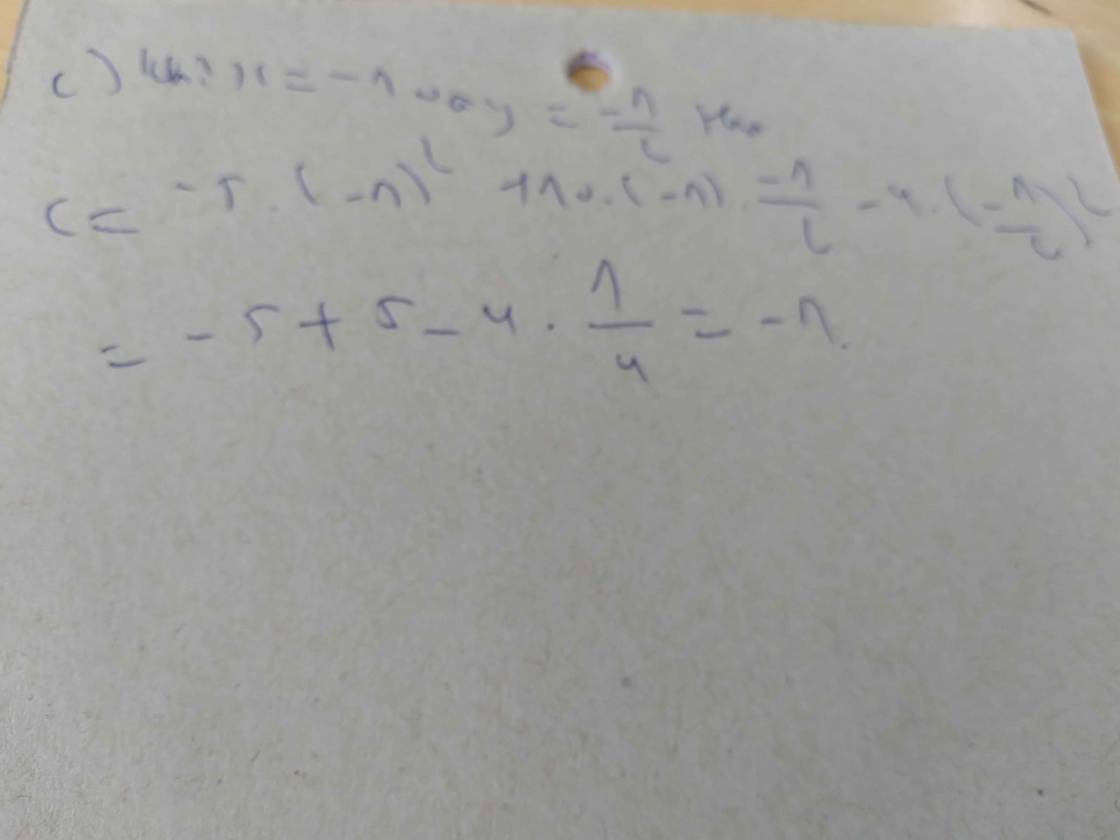

Cho 2 đa thức: f(x)= 9 - x5 + 4x - 2x3 + x2 - 7x4
g(x)= x5 - 9 + 2x2 + 7x4 + 2x3 - 3x
a) Sắp sếp các đa thức trên theo luỹ thừa giảm dần của biến
f(x)= 9 - x5 + 4x - 2x3 + x2 - 7x4
f(x) = -x5 - 7x4 - 2x3 + x2 + 4x + 9
g(x)= x5 - 9 + 2x2 + 7x4 + 2x3 - 3x
g(x) = x5 + 7x4 + 2x3 + 2x2 - 3x - 9
b) Tìm bậc, hệ số cao nhất, hệ số tự do của đa thức f(x); g(x)
f(x) = -x5 - 7x4 - 2x3 + x2 + 4x + 9
+ Bậc : 5 _ hệ số cao nhất : -1 _ hệ số tự do : 9
g(x) = x5 + 7x4 + 2x3 + 2x2 - 3x - 9
+ Bậc : 5_ hệ số cao nhất : 1 _ hệ số tự do : -9
c) Tính f(x) + g(x); f(x) - g(x)
f( x) + g(x) = ( -x5 - 7x4 - 2x3 + x2 + 4x + 9 ) +( x5 + 7x4 + 2x3 + 2x2 - 3x - 9 )
= -x5 - 7x4 - 2x3 + x2 + 4x + 9 + x5 + 7x4 + 2x3 + 2x2 - 3x - 9
= ( -x5 + x5 ) + ( -7x4 + 7x4 ) + ( -2x3 + 2x3 ) + ( x2 + 2x2 ) + ( 4x -3x ) + ( 9 - 9 )
= 3x2 + x
f( x) - g(x) = ( -x5 - 7x4 - 2x3 + x2 + 4x + 9 ) - ( x5 + 7x4 + 2x3 + 2x2 - 3x - 9 )
= -x5 - 7x4 - 2x3 + x2 + 4x + 9 - x5 - 7x4 - 2x3 - 2x2 + 3x + 9
= ( -x5 - x5 ) + ( -7x4 - 7x4 ) + ( -2x3 - 2x3 ) + ( x2 - 2x2 ) + ( 4x + 3x ) + ( 9 + 9 )
= -2x5 - 14x4 - 2x3 -x2 + 7x + 18

a, A=\(-5x^2-2y^2+9xy\)
B= \(6x^2-2y^2+xy\)
b, C= \(1x^2+10xy\)
\(A=-7x^2-3y^2+9xy-2x^2+y^2.\)
\(=\left(-7x^2-2x^2\right)+\left(-3y^2+y^2\right)+9xy\)
\(=-9x^2-2y^2+9xy\)
\(B=5x^2+xy-x^2-2y^2\)
\(=\left(5x^2-x^2\right)-2y^2+xy\)
\(=4x^2-2y^2+xy\)
\(C=\left(-9x^2-2y^2+9xy\right)+\left(4x^2-2y^2+xy\right)\)
\(=\left(-9x^2+4x^2\right)+\left(-2y^2-2y^2\right)+\left(9xy+xy\right)\)
\(=-5x^2-4y^2+10xy\)

a)
A= -7x2 - 3y2 + 9xy - 2x2 + y2
= (-7x2 - 2x2) + (-3y2 + y2) + 9xy
= -9x2 - 2y2 + 9xy
B= 5x2 + xy - x2 - 2y2
= (5x2 - x2) - 2y2 + xy
= 4x2 - 2y2 + xy
b)
C= A +B = (-9x2 - 2y2 + 9xy) + (4x2 - 2y2 + xy)
= -9x2 - 2y2 + 9xy + 4x2 -2y2 + xy
= (-9x2 + 4x2) + (-2y2 -2y2) + (9xy + xy)
C = -5x2 -4y2 +10xy
a) \(A=-7x^2-3y^2+9xy-2x^2+y^2\)
\(\Leftrightarrow A=\left(-7x^2-2x^2\right)-\left(3y^2-y^2\right)+9xy\)
\(\Leftrightarrow A=-9x^2-2y^2+9xy\)
\(B=5x^2+xy-x^2-2y^2\)
\(\Leftrightarrow B=\left(5x^2-x^2\right)-2y^2+xy\)
\(\Leftrightarrow B=4x^2-2y^2+xy\)
b) \(C=A+B\)
\(\Leftrightarrow C=-9x^2-2y^2+9xy+4x^2-2y^2+xy\)
\(\Leftrightarrow C=\left(-9x^2+4x^2\right)-\left(2y^2+2y^2\right)+\left(9xy+xy\right)\)
\(\Leftrightarrow C=-5x^2-4y^2+10xy\)

A + B = (2x^2 y^2 - 4x^3 + 7xy - 18) + (x^3y + x^2y^2 - 15xy + 1)
= 2x^2 y^2 - 4x^3 + 7xy - 18 + x^3y + x^2y^2- 15xy + 1
= (2x^2 y2 + x^2y^2) - 4x^3 + x^3y + (7xy – 15xy) + ( -18 + 1)
= 3x^2 y2 - 4x^3 + x^3y – 8xy – 17