Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


d: Xét ΔABC có
BK,CH là đường cao
BK cắt CH tại I
=>I là trực tâm
=>AI vuông góc BC
mà HF vuông góc BC
nên AI//HF
e: Xét ΔABC cân tại A có góc BAC=60 độ
nên ΔABC đều
Xét ΔABC đều có I là trực tâm
nên I là tâm đường tròn ngoại tiếp ΔABC
=>IA=IB=IC

`d)\sqrt{2+\sqrt{2+\sqrt{x}}}=2` `ĐK: x >= 0`
`=>2+\sqrt{2+\sqrt{x}}=4`
`=>\sqrt{2+\sqrt{x}}=2`
`=>2+\sqrt{x}=4`
`=>\sqrt{x}=2`
`=>x=4` (t/m)
Vậy `x=4`

Bài 19:
a: \(A=5x+\dfrac{1}{9}y=5\cdot\dfrac{-1}{10}+\dfrac{1}{9}\cdot4.8=\dfrac{-1}{2}+\dfrac{8}{15}=\dfrac{-15+16}{30}=\dfrac{1}{30}\)
b: \(A=x-\dfrac{2}{3}=\dfrac{-1}{3}-\dfrac{2}{3}=-1\)
\(a,7x-2x-\dfrac{2}{3}y+\dfrac{7}{9}y=5x+\dfrac{1}{9}y\\ =5.\left(\dfrac{-1}{10}\right)+\dfrac{1}{9}.4,8\\ =\dfrac{-1}{2}+\dfrac{8}{15}=\dfrac{1}{30}\\ b,x=\dfrac{0,2-0,375+\dfrac{5}{11}}{-0,3+\dfrac{9}{16}-\dfrac{15}{22}}\\ =\dfrac{-1}{3}+\dfrac{\dfrac{-7}{40}+\dfrac{5}{11}}{\dfrac{21}{80}-\dfrac{15}{22}}\\ =\dfrac{-1}{3}+\dfrac{\dfrac{123}{440}}{\dfrac{-369}{880}}=\dfrac{-1}{3}+\dfrac{-2}{3}=\dfrac{-3}{3}=\left(-1\right)\)

a: góc ABC=90 độ-góc ACB
góc KHC=90 độ-góc ACB
=>góc ABC=góc KHC
b: Xét ΔBAH vuông tại A và ΔBKH vuông tại K có
BH chung
góc ABH=góc KBH
=>ΔBAH=ΔBKH
=>BA=BK và HA=HK
=>BH là trung trực của AK
c: Xét ΔIBC có
BD,CA là đường cao
BD căt CAt tại H
=>H là trực tâm
=>I,H,K thẳng hàng
d: ΔADK đều
=>góc ADH=30 độ
=>góc AIK=30 độ
=>góc ABC=60 độ

d: Xét ΔABK và ΔCKB có
AB=CK
KB chung
AK=CB
Do đó: ΔABK=ΔCKB

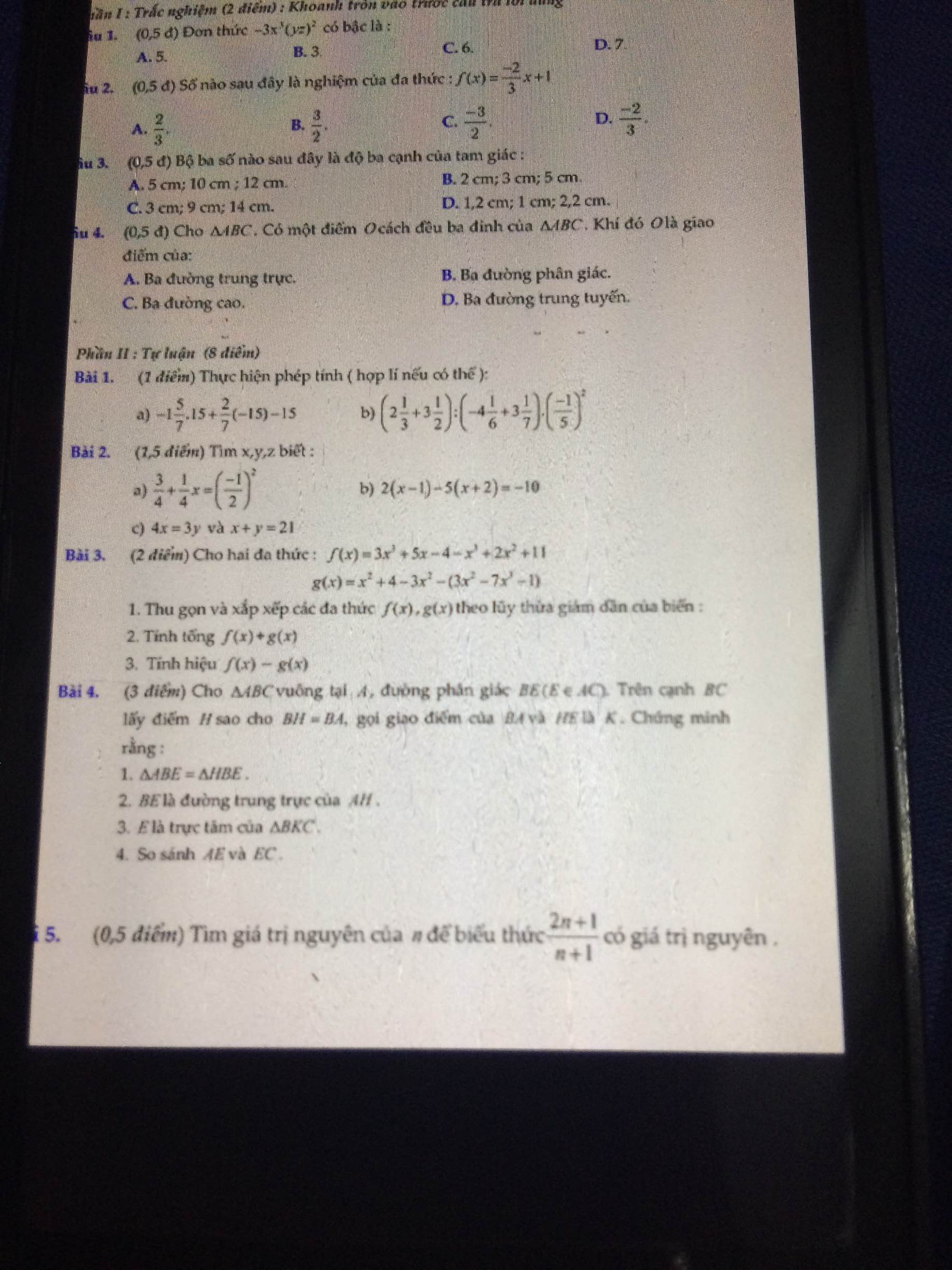
Bài 4:
a) Xét ΔABE và ΔHBE có
BA=BH(gt)
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
BE chung
Do đó: ΔABE=ΔHBE(c-g-c)
b) Ta có: ΔABE=ΔHBE(cmt)
nên EA=EH(hai cạnh tương ứng)
Ta có: BA=BH(gt)
nên B nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: EA=EH(cmt)
nên E nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BE là đường trung trực của AH
c) Ta có: ΔABE=ΔHBE(cmt)
nên \(\widehat{BAE}=\widehat{BHE}\)(hai góc tương ứng)
mà \(\widehat{BAE}=90^0\)(gt)
nên \(\widehat{BHE}=90^0\)
Xét ΔBKC có
KH là đường cao ứng với cạnh BC
CA là đường cao ứng với cạnh BK
KH cắt CA tại E
Do đó: E là trực tâm của ΔBKC(Tính chất ba đường cao của tam giác)
d) Ta có: EA=EH(cmt)
mà EH<EC(ΔEHC vuông tại H có EC là cạnh huyền)
nên EA<EC

\(\frac{1}{12}-\left(-\frac{1}{6}-\frac{1}{4}\right)\)
\(=\frac{1}{12}-\left(-\frac{2}{12}-\frac{3}{12}\right)\)
\(=\frac{1}{12}+\frac{2}{12}+\frac{3}{12}\)
\(=\frac{1}{2}\)
Thanks bạn cute Jeon Koo Koo nhìu nha , tớ cảm ơn pạn rất nhìu :3

127^2 + 146 x 126 + 73^2
= 127^2 + 2 x 73 x 126 + 73 x 73
= 127^2 + 73 x ( 2 x126 + 73 )
=......
rồi sau đo tinh binh thuong mk chi co the giup vay thoi

Ta có :
\(\frac{x-3}{97}+\frac{x-27}{73}+\frac{x-67}{33}+\frac{x-73}{27}=4\)
\(\Leftrightarrow\left(\frac{x-3}{97}-1\right)+\left(\frac{x-27}{73}-1\right)+\left(\frac{x-67}{33}-1\right)+\left(\frac{x-73}{27}-1\right)=0\)
\(\Leftrightarrow\frac{x-100}{97}+\frac{x-100}{73}+\frac{x-100}{33}+\frac{x-100}{27}=0\)
\(\Leftrightarrow\left(x-100\right)\left(\frac{1}{97}+\frac{1}{73}+\frac{1}{33}+\frac{1}{27}\right)=0\)
Vì \(\frac{1}{97}+\frac{1}{73}+\frac{1}{33}+\frac{1}{27}>0\) Nên \(x-100=0\)
\(\Leftrightarrow x=100\)
Vậy \(x=100\)
\(\Leftrightarrow\frac{x-3}{87}+\frac{x-27}{79}+\frac{x-67}{33}+\frac{x-73}{27}-4=0\)
\(\Leftrightarrow\left(\frac{x-3}{97}-1\right)+\left(\frac{x-27}{73}-1\right)+\left(\frac{x-67}{33}-1\right)+\left(\frac{x-73}{27}-1\right)=0\)
\(\Leftrightarrow\left(\frac{x-3-97}{97}\right)+\left(\frac{x-27-73}{73}\right)+\left(\frac{x-67-33}{33}\right)+\left(\frac{x-73-27}{27}\right)=0\)
\(\Leftrightarrow\frac{x-100}{97}+\frac{x-100}{73}+\frac{x-100}{33}+\frac{x-100}{27}=0\)
\(\Leftrightarrow\left(x-100\right)\left(\frac{1}{97}+\frac{1}{73}+\frac{1}{33}+\frac{1}{27}\right)=0\)
Vì \(\frac{1}{97}+\frac{1}{73}+\frac{1}{33}+\frac{1}{27}\ne0\)
\(\Rightarrow x-100=0\Leftrightarrow x=100\)




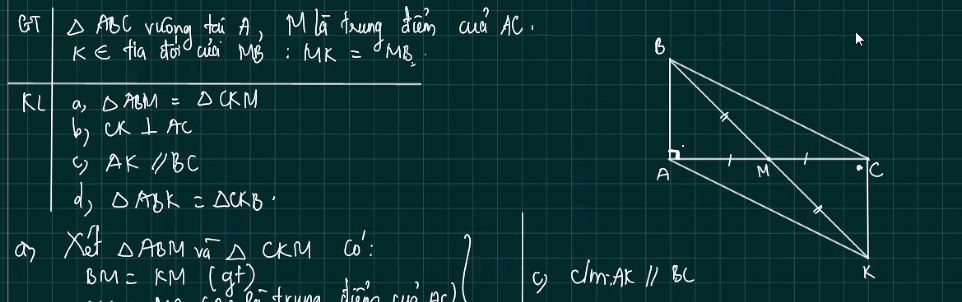 giúp mình câu d với
giúp mình câu d với