Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
· Trong tam giác ABC thì MP là đường trung bình nên”
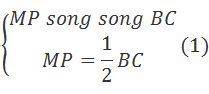
· Trong tam giác OBC ta có MP là đường trung bình nên:
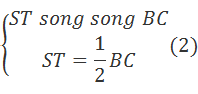
![]()
Suyra:MPTS là hình bình hành. (*)
Ta kiếm góc vuông:
Trong tam giác COA ta có TP là đường trung bình nên TP//AO
=>![]() (3)
(3)
Trong tam giác ABC ta có MP là đường trung bình nên MP//BC
=>![]() (4)
(4)
Từ (3),(4) suy ra: ![]()
Suy ra; ![]()
Từ(*),(**) suy ra MPTS là hình chử nhật.
=>MT=PS và chúng cắt nhau tại trung điểm. (5)
b) chứng minh tương tự câu a ta cũng có:
RPNS là hình chử nhật ,do đó:
RN=PS, và chúng cắt nhau tại trung điểm. (6)
Từ (5),(6), suy ra 3 đoạn RN,MT,SP bằng nhau và cắt nhau tại trung điểm mỗi đường

Dễ thấy MN là đường trung bình của tam giác ABC
Do đó MN//AC và MN=1/2.AC
Tương tự: DF là đtb của tam giác AHC. Suy ra DF//AC,DF=1/2.AC
Mặt khác: góc MDH+góc CDH=góc BHC+góc HAC=90^0
Do đó tứ giác MNFD là hcn.
chứng minh tương tự ta cũng sẽ có:MEFP là hcn.
P/s: Do mới xài nên chả biết up cái ảnh ở đâu nên bạn tự vẽ hình nhé
a) Ta có:
· Trong tam giác ABC thì MP là đường trung bình nên”
· Trong tam giác OBC ta có MP là đường trung bình nên:
Suyra:MPTS là hình bình hành. (*)
Ta kiếm góc vuông:
Trong tam giác COA ta có TP là đường trung bình nên TP//AO
=>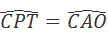 (3)
(3)
Trong tam giác ABC ta có MP là đường trung bình nên MP//BC
=>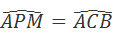 (4)
(4)
Từ (3),(4) suy ra:
Suy ra;
Từ(*),(**) suy ra MPTS là hình chử nhật.
=>MT=PS và chúng cắt nhau tại trung điểm. (5)
b) chứng minh tương tự câu a ta cũng có:
RPNS là hình chử nhật ,do đó:
RN=PS, và chúng cắt nhau tại trung điểm. (6)
Từ (5),(6), suy ra 3 đoạn RN,MT,SP bằng nhau và cắt nhau tại trung điểm mỗi đường