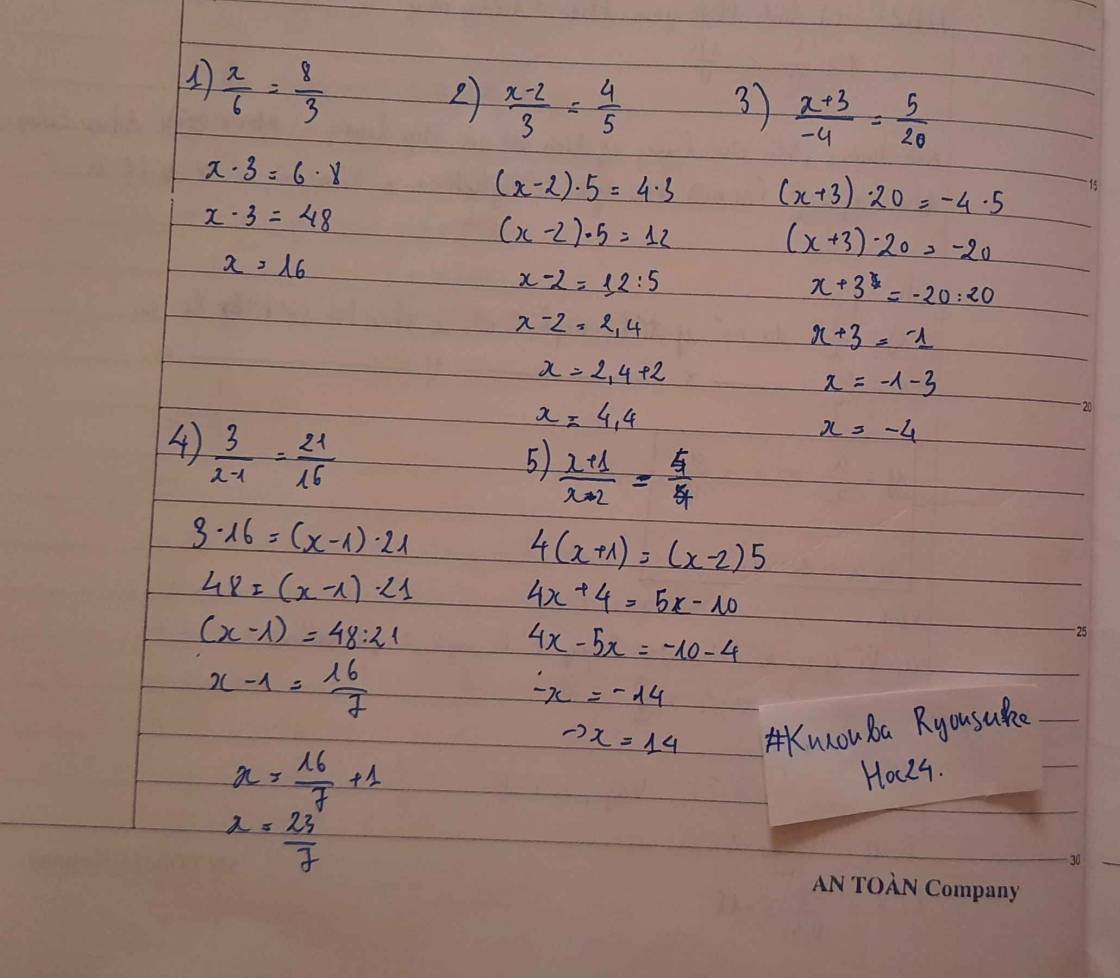Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔOEA và ΔOEB có
OE chung
EA=EB
OA=OB
=>ΔOEA=ΔOEB
Xét ΔOAF và ΔOBF có
OA=OB
AF=BF
OF chung
=>ΔOAF=ΔOBF
b: OA=OB
=>O nằm trên trung trực của AB(1)
EA=EB
nên E nằm trên trung trực của AB(2)
FA=FB
=>F nằm trên trung trực của AB(3)
Từ (1), (2), (3) suy ra O,E,F thẳng hàng

Bài 6:
a: Xét ΔOAE vuông tại A và ΔOBF vuông tại B có
OA=OB
góc O chung
=>ΔOAE=ΔOBF
=>AE=BF
b: Xet ΔIAF vuông tại A và ΔIBE vuông tại B có
AF=BE
góc IFA=góc IEB
=>ΔIAF=ΔIBE
c: ΔIAF=ΔIBE
=>IA=IB
Xét ΔOAI và ΔOBI có
OI chung
OA=OB
IA=IB
=>ΔOAI=ΔOBI
=>góc AOI=góc BOI
=>OI là phân giác của góc xOy

Bài 2:
1: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x+y}{3+4}=\dfrac{14}{7}=2\)
=>x=6; y=8
2: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{5}=\dfrac{y}{2}=\dfrac{3x-2y}{3\cdot5-2\cdot2}=\dfrac{44}{11}=4\)
=>x=20; y=8
3: Đặt x/3=y/4=k
=>x=3k; y=4k
x^2+y^2=100
=>25k^2=100
=>k^2=4
TH1: k=2
=>x=6; y=8
TH2: k=-2
=>x=-6; y=-8
4: Đặt x/4=y/3=k
=>x=4k; y=3k
xy=12
=>12k^2=12
=>k^2=1
TH1: k=1
=>x=4; y=3
TH2: k=-1
=>x=-4; y=-3
5: 4x=3y
=>x/3=y/4=k
=>x=3k; y=4k
x^2+y^2=100
=>9k^2+16k^2=100
=>25k^2=100
=>k^2=4
TH1: k=2
=>x=6; y=8
TH2: k=-2
=>x=-6; y=-8
5: 2x=5y
=>x/5=y/2=k
=>x=5k; y=2k
x^3+y^3=133
=>125k^3+8k^3=133
=>k=1
=>x=5; y=2

Bài tham khảo:
Một tam giác vuông có các cạnh góc vuông tỉ lệ với 7 và 24, chu vi bằng 112 cm. Tính độ dài cạnh huyền ?
2 câu trả lờiGọi b, c là độ dài các cạnh góc vuông,a là độ dai cạnh huyền (tính bằng cm). Ta có:
b7=c24=k⇒b=7k,c=24kb7=c24=k⇒b=7k,c=24k
Theo định lí Py-ta-go:
a2 = b2 + c2 = (7k)2 + (24k)2 = 625k2 = (25k)2
nên a = 25k
Theo đề bài a + b + c = 112 (cm). Từ đó ta tính được k = 2. Vậy a = 50cm.


Lời giải:
$x-y=2\Rightarrow x=y+2$. Thay vào biểu thức $Q$ ta có:
$Q=(x-y)^2+xy=4+xy=4+y(y+2)=y^2+2y+4=(y+1)^2+3\geq 3$
Vậy $Q_{\min}=3$.
Giá trị này đạt được khi $y+1=0\Leftrightarrow y=-1; x=1$

3^x - 2 = 81
3^x = 81 +2
3^x = 83
bạn tự quy nốt về để có cơ số là 3 nhé !!! ( bạn chắc đề bài đúng ko )

\(2.16\ge2^n>4\)
\(2.2^4\ge2^n>2^2\)
\(2^5\ge2^n>2^2\)
=> \(n\in\left\{3,4,5\right\}\)
Vậy: \(n\in\left\{3,4,5\right\}\)