Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chứng minh rằng các đường trung tuyến của tam giác chia tam giác thành 6 phần có diện tích bằng nhau


Vẽ 1 hình tam giác đều có 3 đường trung tuyến nối từ đỉnh A,B,C đến lần lượt các điểm N,L,D sau đó tam giác được chia thành sáu phần
Vì đường trung tuyến luôn chia nửa hình tam giác thành 2 phần bằng nhau.
=> TH1: Đỉnh A: 1+6+5=2+3+4
TH2: Đỉnh B: 6+1+2=5+4+3
TH3: Đỉnh C: 1+2+3=4+5+6
====>1=6=2
5=4=3
6=5=4
1=2=3
1=6=5
2=3=4
=>> tất cả đều bằng nhau

bn tự vẽ hình nha
+) Tam giác AOB và AOD có chung chiều cao hạ từ A xuống BD => S(AOB)/ S(AOD) = OB/OD
+) Tam giác COB và COD có chung chiều cao hạ từ C xuống BD => S(COB)/ S(COD) = OB/OD
=> S(AOB)/S(AOD) = S(COB)/ S(COD)
=> S(AOB). S(COD) = S(AOD).S(COB)
=> S(AOB).S(BOC).S(COD). (DOA) = [S(AOD).S(COB)]2 là số chính phương Vì S(AOD) và S(COB) nguyên
=> đpcm

Theo tính chất trung tuyến, suy ra:
S1 = S2 (có đáy bằng nhau và cùng chiều cao) (1)
S3 = S4 (có đáy bằng nhau và cùng chiều cao) (2)
S5 = S6 (có đáy bằng nhau và cùng chiều cao) (3)
Ta có: S1 + S2 + S3 = S4 + S5 + S6 (= 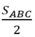 )
)
⇔ 2S1 + S3= S4 + 2S6 ( vì S1= S2; S5 = S6)
⇔ 2S1 = 2S6( vì S3 = S4)
⇔ S1 = S6.
Và S1+ S2+ S6 = S3 + S4 +S5 = 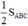 (5)
(5)
Kết hợp (5) với (1), (2), (3) suy ra S2 = S3 (5’)
Và S1 + S5 + S6 = S2+ S3 + S4 = 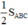 (6)
(6)
Kết hợp (6) với (1), (2), (3) suy ra S4 = S5 (6’)
Từ (4’), (5’), (6’) và kết hợp (1) (2) (3) ta có: S1= S2 = S3 = S4 = S5 = S6


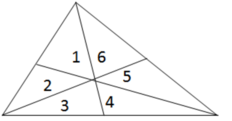

Gọi AM, BN, CL là các trung tuyến của tam giác ABC => G là trọng tâm của tam giác ABC. Ta cần phải chứng minh S(GAB)=S(GBC)=S(GAC). + Hai tam giác AMC và tam giác ABC có chung đường cao hạ từ A xuống BC nên S(AMC)/S(ABC)=MC/BC=1/2 => S(AMC)=S(ABC)/2 (1) + Hai tam giác GAC và tam giác AMC có chung đường cao hạ từ C xuống AM nên S(GAC)/S(AMC)=AG/AM=2/3 (3 đường trung tuyến cắt nhau tại 1/3 mmỗi đường kể từ đáy) => S(GAC)=2.S(AMC)/3 (2) Từ (1) và (2) => S(GAC)=S(ABC)/3 + Tương tự cũng c/m được S(GAB)=S(GBC)=S(ABC)/3 => Trọng tâm của tam giác khi nối với đỉnh của tam giác ABC thì chia tam giác ABC thành 3 tam giác nhỏ có diện tích bằng nhau
Chúc bạn học tốt 🙆♀️❤