Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trường hợp A và B nằm trên một nửa mặt phẳng bờ chứa đường thẳng d.
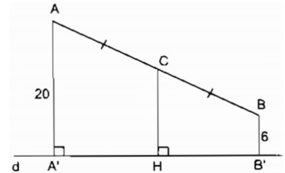
Gọi A', B' là chân đường vuông góc kẻ từ A và B đến d
AA' ⊥ d; BB' ⊥ d ⇒ AA' // BB'
Tứ giác ABB'A' là hình thang. Kẻ CH ⊥ d
⇒ CH // AA' // BB' nên CH là đường trung bình của hình thang ABB'A'
⇒CH = (AA'+BB')/2 = (20 + 6)/2 = 13 (cm)

Trường hợp A và B nằm trên hai nửa mặt phẳng đối bờ chứa đường thẳng d
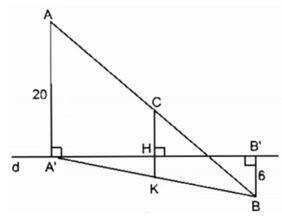
Kẻ CH ⊥ d cắt A'B tại K
⇒ CH // AA' // BB'
Trong ∆ AA'B ta có: AC = CB
Mà CK // AA' nên A'K = KB và CK là đường trung bình của tam giác AA'B
⇒CK= AA'/2 (tính chất đường trung bình của tam giác)
CK = 20/2 = 10(cm)
Trong ∆ A'BB' có A'K = KB và KH // BB'
Nên KH là đường trung bình của ∆ A'BB'
⇒ KH = BB'/2 (tính chất đường trung bình của tam giác)
⇒ KH = 6/2 =3 (cm)
CH = CK – KH = 10 – 3 = 7(cm)


Xét hai trường hợp :
- Trường hợp A và B nằm cùng phía đối với đường thẳng d (h.bs.6a). Ta tính được :
\(CH=\dfrac{20+6}{2}=13\left(cm\right)\)
- Trường hợp A và B nằm khác phía đối với đường thẳng d (h.bs.6b). Ta tính được :
\(CH=CK-HK=10-3=7\left(cm\right)\)

Gọi khoảng cách từ A,B,C đến d theo thứ tự là D,E,F
Ta có \(AD//BE\left(\perp d\right)\) nên ABED là hình thang
Mà \(AC=CB;AD//BE//CF\left(\perp d\right)\) nên \(DF=FE\)
Do đó CE là đường trung bình hình thang ABED
\(\Rightarrow CE=\dfrac{AD+BE}{2}=\dfrac{18}{2}=9\left(cm\right)\)
Vậy k/c từ C đến d là 9 cm

A C B I H K
Hình vẽ hơi xấu trìn hbafy nhớ vẽ đẹp =)
Gọi H,I,K lần lượt là các chân cao đường cao của A,C,B đường thẳng d,AH = 12cm BK= 16cm
=> CI là khoản cách từ C đến đường thẳng d
Ta thấy ABKH là hình thang nằm nghiêng (có thể quan sát hình) (đáy AH và BK) là đường trung bình CI
Từ đó \(\frac{\left(AH+BK\right)}{2}=\frac{\left(12+16\right)}{2}=14cm\)
A B C d
ta có khoảng cách giữa A và B là: 20+6=26(cm)
độ dài từ A đến C là
26:2=13(cm)
khoảng cách từ C đến đuờg thẳng d là:
20-13=7(cm)