Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhiệt lượng cần thiết để đun sôi nước:
\(Q_1=\dfrac{U^2}{R_1}\cdot t_1=\dfrac{U^2}{R_2}\cdot t_2\)
\(\Rightarrow\dfrac{t_1}{t_2}=\dfrac{R_1}{R_2}=\dfrac{10}{20}=\dfrac{1}{2}\) \(\Rightarrow R_2=2R_1\)
Nếu dùng cả hai cuộn cuộn dây mắc R1 và R2 nối tiếp để đung lượng nước trên:
\(Q_2=\dfrac{U^2}{R_1+R_2}\cdot t_3=\dfrac{U^2}{3R_1}\cdot t_3\)
Mặt khác: \(Q_1=Q_2\) \(\Rightarrow t_1=\dfrac{t_3}{3}\Rightarrow t_3=30\)(phút)

Chọn đáp án A
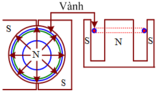
Tại mỗi điểm của vành kinh loại, cảm ứng từ có trị số bằng B. Xét một phần tử chiều dài Δℓ của vành. Tại thời điểm t mà tốc độ của vành là v thì suất điện động ở Δℓ có độ lớn bằng: BvΔℓ. Suấ điện động cảm ứng suất hiện trong toàn bộ vành là
e c u = B v ∑ Δ l = B v .2 π r
⇒ i c u = e c u R = B v .2 π r ρ . 2 π r S = B v S ρ





* Trường hợp 1: Khoảng cách giữa 2 kim lớn hơn 0.
Bài toán: Bây giờ là 7 giờ. Hỏi sau ít nhất bao lâu kim phút lại trùng lên kim giờ ?
Phân tích: Kim phút và kim giờ chuyển động vòng tròn nên đây là dạng toán chuyển động cùng chiều đuổi nhau. Muốn biết được sau ít nhất bao lâu kim phút lại trùng lên kim giờ ? Ta hướng dẫn học sinh theo các bước cụ thể sau:
- Giáo viên cho học sinh quan sát vị trí của kim phút và kim giờ trên đồng hồ thật để trả lời câu hỏi:
(?) Vào lúc 7 giờ, kim phút và kim giờ nằm ở vị trí nào ?
(Kim phút chỉ số 12, kim giờ chỉ số 7)
(?)Khoảng cách giữa kim phút và kim giờ lúc đó là bao nhiêu ?
(7/12 vòng đồng hồ)
(?) Đến khi kim phút và kim giờ trùng khít lên nhau thì khoảng cách giữa hai kim là bao nhiêu ?
(Bằng 0)
(?) Lúc đó kim phút đã đi hơn kim giờ đoạn đường bằng bao nhiêu ?
(Lúc đó kim phút đã đi nhiều hơn kim giờ một đoạn đường đúng bằng khoảng cách giữa hai kim đồng hồ lúc 7 giờ đúng, nghĩa là bằng 7/12 vòng đồng hồ).
(?) Mỗi giờ kim phút và kim giờ đi được bao nhiêu ?
(Cứ mỗi giờ kim phút đi được 1 vòng đồng hồ còn kim giờ chỉ đi được 1/12 vòng đồng hồ nên trong một giờ kim phút đi nhanh hơn kim giờ là: 1 – 1/12 = 11/12 vòng đồng hồ.
Như vậy đây là chính là dạng toán “Hai động tử chuyển động cùng chiều đuổi nhau” có khoảng cách ban đầu là 7/12 vòng đồng hồ và hiệu hai vận tốc là 11/12 vòng đồng hồ. Từ sự hướng dẫn, phân tích đó học sinh sẽ vận dụng và giải bài toán như sau:
Bài giải:
Trong một giờ kim phút đi được 1 vòng đồng hồ thì kim giờ sẽ đi được 1/12 vòng đồng hồ. Vậy hiệu vân tốc giữa kim phút và kim giờ là:
1 - 1/12 = 11/12 (vòng đồng hồ/giờ)
Lúc 7 giờ kim giờ cách kim phút 7/12 vòng đồng hồ.
Khoảng thời gian ngắn nhất để kim phút lại trùng với kim giờ là:
7/12 : 11/12 = 7/11 (giờ)
Đáp số: 7/11 giờ
Cách tính: Lấy khoảng cách giữa 2 kim chia cho hiệu vận tốc của chúng.
* Trường hợp 2: Khoảng cách giữa 2 kim bằng 0.
Bài toán: Bây giờ là 12 giờ, ít nhất sau bao lâu hai kim đồng hồ sẽ chập nhau ?
Phân tích: Ta nhận thấy lúc 12 giờ khoảng cách giữa hai kim là bằng 0 nên ta hướng dẫn học sinh giải theo các bước sau:
Bài giải:
Lúc 12 giờ, hai kim đồng hồ cùng chỉ vào số 12. Vì kim phút đi nhanh hơn kim giờ nên kim phút đi hết một vòng đồng hồ tức là 1 giờ mà hai kim vẫn chưa gặp nhau, lúc này là 1 giờ đúng.
Lúc 1 giờ kim phút chỉ vào số 12, kim giờ chỉ vào số 1. Khoảng cách lúc này giữa hai kim là 1/12 vòng đồng hồ.
Hiệu vận tốc của hai kim là:
1 – 1/12 =11/12 (vòng đồng hồ/giờ).
Kể từ lúc 1 giờ, thời gian để kim phút đuổi kịp kim giờ là:
1/12 : 11/12 = 1/11 (giờ)
Kể từ lúc 12 giờ, thời gian để hai kim chập nhau là:
1 + 1/11 = 12/11 (giờ)
Đáp số : 12/11 giờ
Cách tính: Lấy 1 cộng với số thời gian ít nhất để hai kim trùng khít lên nhau biết hiện tại lúc đó là 1 giờ đúng.
Tham khảo đâu?? Sao cứ để nhắc hoài vậy!??!