Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Mỗi mặt của khối lập phương chứa 4 mặt của 4 khối lập phương nhỏ chỉ có 1 mặt được sơn đỏ Vậy số khối lập phương chỉ có 1 mặt được sơn đỏ là 4x6=24.

Chọn D.
Để khối lập phương nhỏ thu được sau khi cắt có có đúng 2 mặt được sơn đỏ thì khối lập phương nhỏ đó phải có một cạnh nằm trên cạnh giao của hai mặt hình lập phương, mà tại các đỉnh thì khối lập phương nhỏ thu được sẽ có 3 mặt được tô đỏ.
=> trên một cạnh của hình lập phương ta sẽ có có 8 khối lập phương nhỏ thỏa mãn đề. Vì hình lập phương có tất cả 12 cạnh nên số khối lập phương thu được sau khi cắt có đúng 2 mặt được sơn đỏ là 8.12=96.

Đáp án là C
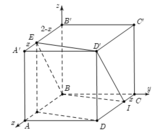
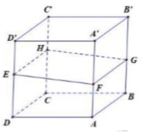
Mặt phẳng (P) cắt hình lập phương theo thiết diện là hình bình hành BID’E.
Hình chiếu vuông góc của bình hành BID’E xuống mặt phẳng (ABCD) là hình bình hành BIDF.
Gọi φ là góc tạo bởi (P) và mặt phẳng (ABCD).
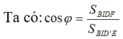
Đặt hình lập phương vào hệ tọa độ như hình vẽ. B ≡ O; Ox ≡ BA; Oy ≡ BC; Oz ≡ BB’
Đặt A’E = x.
![]()
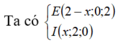
![]()
![]()
![]()
Suy ra
![]()
Khi đó
![]()
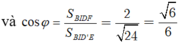

Giải:
a) Mặt phẳng (Oxy) qua điểm O(0 ; 0 ; 0) và có vectơ pháp tuyến (0 ; 0 ; 1) và là vectơ chỉ phương của trục Oz. Phương trình mặt phẳng (Oxy) có dạng:
0.(x - 0) +0.(y - 0) +1.(z - 0) = 0 hay z = 0.
Tương tự phương trình mặt phẳng (Oyz) là : x = 0 và phương trình mặt phẳng (Ozx) là: y = 0.
b) Mặt phẳng (P) qua điểm M(2; 6; -3) song song với mặt phẳng Oxy nhận (0 ; 0 ; 1) làm vectơ pháp tuyến. Phương trình mặt phẳng (P) có dạng: z +3 = 0.
Tương tự mặt phẳng (Q) qua M và song song với mặt phẳng Oyz có phương trình x - 2 = 0.
Mặt phẳng qua M song song với mặt phẳng Oxz có phương trình y - 6 = 0.
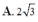
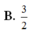
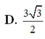


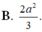
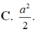


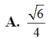
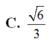

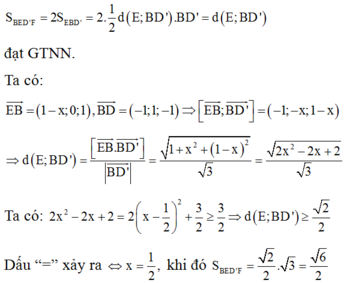

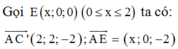
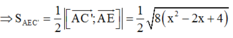
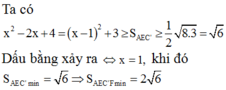
Đáp án C.
Mỗi mặt sẽ có 4 phần thuộc hình chỉ được tô một lần tức là mỗi mặt sẽ sinh ra 4 hình lập phương thỏa mãn yêu cầu bài toán, ta có 6 mặt, từ đó ta có 24 hình thỏa mãn yêu cầu