Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của người đi xe máy trên 3/4 quãng đường AB đầu (90 km) là x (km/h) (x > 0)
Vận tốc của người đi xe máy trên 1/4 quãng đường AB sau là 0,5x (km/h)
Vận tốc của người đi xe máy khi quay trở lại A là x + 10 (km/h)
Tổng thời gian của chuyến đi là 90 x + 30 0 , 5 x + 120 x + 10 + 1 2 = 8 , 5
⇔ 90 x + 60 x + 120 x + 10 = 8 ⇔ 150 x + 120 x + 10 = 8 ⇔ 75 ( x + 10 ) + 60 x = 4 x ( x + 10 ) ⇔ 4 x 2 − 95 x − 750 = 0 ⇔ x = 30 ( d o x > 0 )
Vậy vận tốc của xe máy trên quãng đường người đó đi từ B về A là 30 + 10 = 40 (km/h)

Đáp án D
Gọi vận tốc của ô tô khi đi từ A đến B là x (km/h) (x > 0)
Thời gian ô tô đi từ A đến B là: 156/x (giờ)
Vận tốc của ô tô lúc về là: x + 32 (km) .
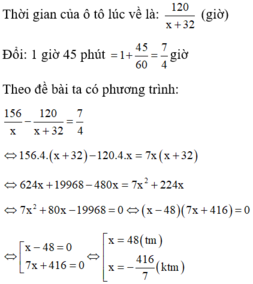
Vậy vận tốc của ô tô lúc đi từ A đến B là 48km/h

Gọi vận tốc của xuồng lúc đi là x (km/h, x > 5).
⇒ Vận tốc của xuồng lúc về là x – 5 (km/h).
Thời gian đi là: 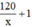 (h)
(h)
Quãng đường về là: 120 + 5 = 125 km
Thời gian về là: 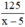 (h)
(h)
Theo bài ra ta có phương trình:
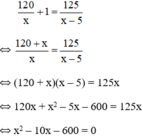
Có a = 1; b = -10; c = -600 ⇒ Δ’ = (-5)2 – 1.(-600) = 625
Phương trình có hai nghiệm phân biệt:
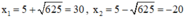
Trong hai nghiệm chỉ có nghiệm x = 30 thỏa mãn điều kiện.
Vậy vận tốc xuồng lúc đi là 30 km/h.

Gọi vận tốc của xuồng lúc đi là x (km/h, x > 5).
⇒ Vận tốc của xuồng lúc về là x – 5 (km/h).
Thời gian đi là: 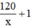 (h)
(h)
Quãng đường về là: 120 + 5 = 125 km
Thời gian về là: 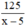 (h)
(h)
Theo bài ra ta có phương trình:
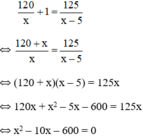
Có a = 1; b = -10; c = -600 ⇒ Δ ’ = ( - 5 ) 2 – 1 . ( - 600 ) = 625
Phương trình có hai nghiệm phân biệt:
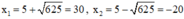
Trong hai nghiệm chỉ có nghiệm x = 30 thỏa mãn điều kiện.
Vậy vận tốc xuồng lúc đi là 30 km/h.
Kiến thức áp dụng
Để giải bài toán bằng cách lập phương trình ta làm theo các bước:
Bước 1: Lập phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Đối chiếu điều kiện rồi kết luận.

Gọi vận tốc lúc đi là x (km/h), x>10
Thời gian đi: \(\dfrac{300}{x}\) giờ
Vận tốc lúc về: \(x-10\)
Thời gian về: \(\dfrac{300}{x-10}\)
Ta có pt: \(\dfrac{300}{x-10}-\dfrac{300}{x}=1\Leftrightarrow300x-300\left(x-10\right)=x\left(x-10\right)\)
\(\Leftrightarrow x^2-10x-3000=0\Rightarrow\left[{}\begin{matrix}x=60\\x=-50\left(loại\right)\end{matrix}\right.\)
Gọi x(km/h) là vận tốc lúc đi(Điều kiện: x>0 và \(x\ne10\))
Thời gian ô tô đi từ A đến B là:
\(\dfrac{300}{x}\)(giờ)
Thời gian ô tô đi từ B về A là:
\(\dfrac{300}{x-10}\)(giờ)
Vì thời gian về nhiều hơn thời gian đi là 1 giờ nên ta có phương trình:
\(\dfrac{300}{x-10}-\dfrac{300}{x}=1\)
\(\Leftrightarrow\dfrac{300x}{x\left(x-10\right)}-\dfrac{300\left(x-10\right)}{x\left(x-10\right)}=\dfrac{x\left(x-10\right)}{x\left(x-10\right)}\)
Suy ra: \(300x-300x+3000=x^2-10x\)
\(\Leftrightarrow x^2-10x-3000=0\)
\(\Leftrightarrow x^2-60x+50x-3000=0\)
\(\Leftrightarrow x\left(x-60\right)+50\left(x-60\right)=0\)
\(\Leftrightarrow\left(x-60\right)\left(x+50\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-60=0\\x+50=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=60\left(nhận\right)\\x=-50\left(loại\right)\end{matrix}\right.\)
Vậy: Vận tốc lúc đi là 60km/h

Gọi vận tốc xe đi \(\frac{3}{4}\)quãng đường đầu là V
Thời gian xe đi \(\frac{3}{4}\)quãng đường đầu là \(\frac{120.3}{4.V}=\frac{90}{V}\)
Vận tốc xe đi \(\frac{1}{4}\)quãng đường sau là \(\frac{V}{2}\)
Thời gian xe đi \(\frac{1}{4}\)quãng đường sau là \(\frac{120.1.2}{4.V}=\frac{60}{V}\)
Vận tốc xe đi từ B về A là \(V+10\)
Thời gian xe đi từ B về A là \(\frac{120}{V+10}\)
Tổng thời gian xe đi là 8,5h nên ta có
\(\frac{90}{V}+\frac{60}{V}+0,5+\frac{120}{V+10}=8,5\)
\(\Leftrightarrow4x^2-95x-750=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=30\\x=\frac{-25}{4}\left(loại\right)\end{cases}}\)
Vậy vận tốc xe chạy từ B về A là 30 + 10 = 40 (km/h)