Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{C}+\widehat{B}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{B}+60^0=90^0\)
hay \(\widehat{B}=30^0\)
Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan\widehat{B}\)
\(\Leftrightarrow AC=10\cdot\tan30^0\)
hay \(AC=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=\left(\dfrac{10\sqrt{3}}{3}\right)^2+10^2=\dfrac{400}{3}\)
hay \(BC=\dfrac{20\sqrt{3}}{3}\left(cm\right)\)

b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AB^2=5.7^2-4.1^2=15,68\)
hay \(AB\simeq3,96\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{41}{57}\)
nên \(\widehat{B}\simeq46^0\)
Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{C}+46^0=90^0\)
hay \(\widehat{C}=44^0\)

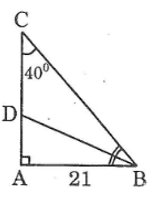
a) Ta có: \(AC=AB.\cot\widehat{C}=21.\cot\widehat{40^o}\simeq25,0268\left(cm\right)\)
b) Ta có: \(BC=\dfrac{AC}{\sin\widehat{C}}=\dfrac{21}{\sin\widehat{40^o}}\simeq32,6702\left(cm\right)\)
c) Vì ΔABCΔABC vuông tại A nên \(\widehat{B}+\widehat{C}=90^o\)
Suy ra: \(\widehat{B}=90^o-\widehat{C}=90^o-40^o=50^o\)
Vì BD là phân giác của B nên:
\(\widehat{ABD}=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}.50^o=25^o\)
Trong tam giác vuông ABD, ta có:
\(BD=\dfrac{AB}{\cos\widehat{ABD}}=\dfrac{21}{\cos25^o}\simeq23,1709\left(cm\right)\)

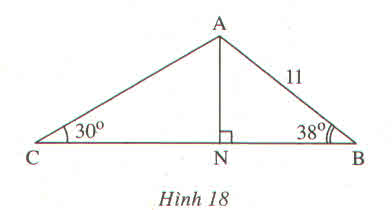
a) Trong tam giác vuông BCH, ta có:
CH=BC.sinB^=12.sin60≈10,392 (cm)
Trong tam giác vuông ABC, ta có:
\(A\)=180−(60+40)=80
Trong tam giác vuông ACH, ta có:
\(AC=\dfrac{CH}{sinA}=\dfrac{10,932}{sin80}=10,552\left(cm\right)\)
b) Kẻ AK⊥BCAK⊥BC
Trong tam giác vuông ACK, ta có:
AK=AC.sinC≈10,552.sin40=6,783 (cm)
Vậy SABC=12.AK.BC≈12.6,783.12=40,696 (cm2)

mình chỉ biết bài 3 thôi. hai bài kia cx làm được nhưng ngại trình bày
A B C 4 9
Ta có : BC = BH +HC = 4 + 9 = 13 (cm)
Theo hệ thức lượng trong tam giác vuông ta có:
- AC2 = BC * HC
AC2 = 13 * 9 = 117
AC = \(3\sqrt{13}\)(cm)
- AB2 =BH * BC
AB2 = 13 * 4 = 52
AB = \(2\sqrt{13}\)(CM)

Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)

Xét ΔANB vuông tại N có
\(AN=AB\cdot\sin B\)
nên \(AN\simeq6,772\left(cm\right)\)
XétΔACN vuông tại N có
\(AC=\dfrac{AN}{\sin C}=13,544\left(cm\right)\)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AB^2=5.7^2-4.1^2=15,68\left(cm\right)\)
hay \(AB=\dfrac{14\sqrt{2}}{5}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{14\sqrt{2}}{5}:\dfrac{57}{10}=\dfrac{28\sqrt{2}}{57}\)
hay \(\widehat{C}\simeq44^0\)
Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{C}+\widehat{B}=90^0\)
hay \(\widehat{B}=46^0\)
cách nào để tính từ sin \(\widehat{C}\)
chuyền sang \(^{\widehat{C}}\) vậy ạ?