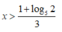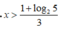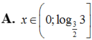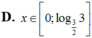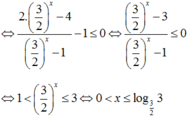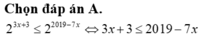DT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KD
0
HT
20 tháng 5 2016
\(5^{1+x^2}-5^{1-x^2}>24\Leftrightarrow5\times5^{x^2}-\frac{5}{5^{x^2}}>24\) (1)
Đặt \(t=5^{x^2}\), dk: \(t>0\)
\(\left(1\right)\Leftrightarrow5t-\frac{5}{t}>24\Leftrightarrow5t^2-24t-5>0\Leftrightarrow\left[\begin{array}{nghiempt}t< \frac{-1}{5}\left(loai\right)\\t>5\end{array}\right.\)\(\Leftrightarrow5^{x^2}>5\Leftrightarrow x^2>1\Leftrightarrow\left[\begin{array}{nghiempt}x< -1\\x>1\end{array}\right.\)
CM
24 tháng 4 2018
Điều kiện. x≥1/3
Ta có:
2 x 3 + x 2 - 3 x + 1 = 2 ( 3 x - 1 ) 3 x - 1 ⇔ 2 x 3 + x 2 + 1 = 2 ( 3 x - 1 ) 3 + ( 3 x - 1 ) 2 + 1 f ( x ) = f ( 3 x - 1 )
Xét hàm số f(t) = 2t3+ t2+ 1 liên tục tên R.
Ta có: đạo hàm f’ (t) = 6t2+2t> 0 với t>0 .
Do đó ; hàm số f(t) đồng biến trên (0; +∞).
f ( x ) = f ( 3 x - 1 ) ⇔ x = 3 x - 1 ⇔ x 2 = 3 x - 1 ⇔ x = 3 - 5 2 > 1 3 x = 3 + 5 2 > 1 3
Tổng các nghiệm là 3.
Chọn C.
MT
6 tháng 4 2017
Chọn hệ trục tọa độ Oxyz sao cho A)0 ; 0 ; 0), B(1 ; 0 ; 0), D(0 ; 1; 0), A'(0 ; 0 ; 1)
Khi đó
B'(1 ; 0 ; 1), D'(0 ; 1 ; 1), C(1 ; 1 ; 0). Phương trình mặt phẳng (A'BD) có dạng:
x + y + z - 1 = 0. (1)
Ta tìm được phương trình mặt phẳng (B'D'C):
Vectơ: (0 ; -1 ; 1) ;
(-1 ; 0 ; 1).
Mặt phẳng (B'D'C) qua điểm C và nhận = (-1 ; -1 ; -1 ) làm vectơ pháp tuyến. Phương trình mặt phẳng (B'D'C) có dạng:
x + y + z - 2 = 0 (2)
Ta có