Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét ΔBAC vuông tại B có BH là đường cao
nên \(HA\cdot HC=BH^2\left(1\right)\)
Xét ΔBHC vuông tại H có HE là đường cao
nên \(BE\cdot BC=BH^2\left(2\right)\)
Từ (1) và (2) suy ra \(HA\cdot HC=BE\cdot BC\)

A B C O H D E F
Ta có: Tứ giác ABDC nội tiếp đường tròn (O) => ^DBC=^CAD (1)
Đường tròn (O) có đường kính AD và điểm B thuộc (O) => ^ABD vuông tại B => AB \(\perp\)BD
=> HE // BD (Quan hệ song song vuông góc) => ^DBC=^BHE (So le trong)
^BHE=^BAH (Cùng phụ ^AHE) => ^DBC=^BAH=^EAH.
Dễ thấy tứ giác AEHF là tứ giác nội tiếp (Tâm là trung điểm của AH)
=> ^EAH=^EFH. Mà ^EAH=^DBC (cmt) => ^EFH=^DBC (2)
Từ (1) và (2) => ^CAD=^EFH
Lại có: ^EFH+^AFE=900 ; ^CAD+^ADC=900 => ^AFE=^ADC
=> ^CAD+^AFE=900 => AD\(\perp\)EF (đpcm)

Gợi ý: A F E ^ = A H E ^ (tính chất hình chữ nhật và A H E ^ = A B H ^ (cùng phụ B H E ^ )

Ta có: \(\widehat{C_1}=\widehat{A_1}\)(cùng phụ với \(\widehat{B_1}\)) \(\left(1\right)\)
Xét tứ giác AEHF có: \(\widehat{A}=\widehat{E}=\widehat{F}=\widehat{H}=90^o\)
=> tứ giác AEHF là h.c.n
=> \(\widehat{A_1}=\widehat{E_1}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\widehat{E_1}=\widehat{C_1}\)
vì \(\widehat{E_1}+\widehat{BEF}=180^o\)
\(\Rightarrow\widehat{C_1}+\widehat{BEF}=180^o\) mà 2 góc đối nhau
=> tứ giác BEFC nội tiếp

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH=\dfrac{60}{13}\left(cm\right)\)
b: Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)

a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\left(1\right)\)
Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AH^2=AE\cdot AB\left(2\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AH^2=AF\cdot AC\left(3\right)\)
Từ (1), (2) và (3) suy ra \(AE\cdot AB=AF\cdot AC=BH\cdot HC\)

a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(cmt)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔACB(c-g-c)
Suy ra: \(\widehat{AFE}=\widehat{ABC}\)
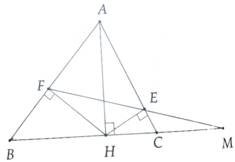
*Gọi D là giao của BM và EF.
△ABC vuông tại B có: BM là trung tuyến.
\(\Rightarrow BM=CM=\dfrac{BC}{2}\)
\(\Rightarrow\)△BMC cân tại M.
\(\Rightarrow\widehat{MCB}=\widehat{MBC}\)
Tứ giác BEHF có: \(\widehat{EBF}=\widehat{BFH}=\widehat{BEH}=90^0\)
\(\Rightarrow\)BEHF là hình chữ nhật.
\(\Rightarrow\widehat{HBE}=\widehat{DEB}\).
Ta có: \(\widehat{MCB}+\widehat{HBE}=90^0\) (△BHC vuông tại H).
\(\Rightarrow\widehat{MBC}+\widehat{DEB}=90^0\)
\(\Rightarrow180^0-\widehat{BDE}=90^0\)
\(\Rightarrow\widehat{BDE}=90^0\)
\(\Rightarrow\)BM⊥EF tại D.
Suppose I is the intersection of BM and EF.
Consider the right triangle ABC, which has \(\widehat{B}=90^o\), has the median BM, so, \(BM=\dfrac{AC}{2}\) (1)
On the other hand, M is the midpoint of AC, therefore, \(AM=\dfrac{AC}{2}\) (2)
From, (1) and (2), we have \(BM=AM\left(=\dfrac{AC}{2}\right)\), which means MAB is an isosceles triangle, and this leads to \(\widehat{A}=\widehat{ABM}\) or \(\widehat{A}=\widehat{FBI}\)
Consider the right triangle ABH (right at H), has the height HF, thus, \(BH^2=BF.BA\)
Similarly, we have \(BH^2=BE.BC\)
From these, we get \(BF.BA=BE.BC\left(=BH^2\right)\) or \(\dfrac{BF}{BC}=\dfrac{BE}{BA}\)
Consider the 2 right triangles (which are both right at B), we have \(\dfrac{BF}{BC}=\dfrac{BE}{BA}\). Therefore, \(\Delta BEF~\Delta BAC\left(s.a.s\right)\), which means \(\widehat{BFE}=\widehat{C}\) or \(\widehat{BFI}=\widehat{C}\)
Also, \(\widehat{A}+\widehat{C}=90^o\) due to the right triangle ABC (right at B). Because \(\widehat{FBI}=\widehat{A};\widehat{BFI}=\widehat{C}\), we have \(\widehat{FBI}+\widehat{BFI}=90^o\). This means FBI is a right triangle (whose right angle is I). Thus, \(BM\perp EF\), and that is what we must prove!