Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

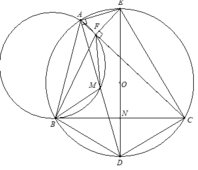
1). Ta có góc nội tiếp bằng nhau B D M ^ = B C F ^ ( 1 ) và B M A ^ = B F A ^ suy ra 180 0 − B M A ^ = 180 0 − B F A ^ hay B M D ^ = B F C ^ (2).
Từ (1) và (2), suy ra Δ B D M ~ Δ B C F (g - g).

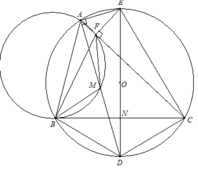
2). Từ AD là phân giác B A C ^ suy ra DB=DC vậy DE vuông góc với BC tại trung điểm N của BC.
Từ 1). Δ B D M ∽ Δ B C F , ta có D M C F = B D B C .
Vậy ta có biến đổi sau D A C F = 2 D M C F = 2 B D B C = C D C N = D E C E (3).
Ta lại có góc nội tiếp A D E ^ = F C E ^ (4).
Từ 3 và 4, suy ra Δ E A D ∽ Δ E F C ⇒ E F C ^ = E A D ^ = 90 ° ⇒ E F ⊥ A C

 .
.
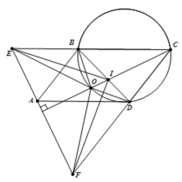
3). Theo trên, ta có B E = C D mà C E = C F ⇒ B C = D F .
Ta có CI là đường phân giác góc BCD, nên I B I D = C B C D = D F B E ⇒ I B . B E = I D . D F .
Mà CO là trung trực EF và I ∈ C O , suy ra IE=IF.
Từ hai đẳng thức trên, suy ra I B . B E . E I = I D . D F . F I .

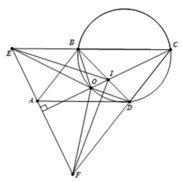
2). Từ Δ O B E = Δ O D C ⇒ O E = O C .
Mà CO là đường cao tam giác cân CEF , suy ra OE=OF.
Từ đó O E = O C = O F , vậy O là tâm đường tròn ngoại tiếp tam giác .

1) Ta có
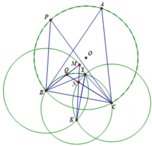
B I C ^ = 180 0 − I B C ^ − I C B ^ = 180 0 − A B C ^ 2 − A C B ^ 2 = 180 0 − 180 ∘ − B A C ^ 2 = 90 0 + B A C ^ 2 ⇔ B A C ^ = 2 B I C ^ − 180 °
Tương tự B Q C ^ = 90 0 + B P C ^ 2 ⇔ B P C ^ = 2 B Q C ^ − 180 ° .
Tứ giác BPAC nội tiếp, suy ra B A C ^ = B P C ^ ⇒ B Q C ^ = B I C ^ , nên 4 điểm B, I, Q, C thuộc một đường tròn.
2) Gọi đường tròn (B; BI) giao (C; CI) tại K khác I thì K cố định.
Góc I B M ^ là góc ở tâm chắn cung I M ⏜ và I K M ^ là góc nội tiếp chắn cung I M ⏜ , suy ra I K M ^ = 1 2 I B M ^ (1).
Tương tự I K N ^ = 1 2 I C N ^ (2).
Theo câu 1) B, I, Q, C thuộc một đường tròn, suy ra I B M ^ = I B Q ^ = I C Q ^ = I C N ^ (3).
Từ (1), (2) và (3), suy ra I K M ^ = I K N ^ ⇒ K M ≡ K N .
Vậy MN đi qua K cố định.

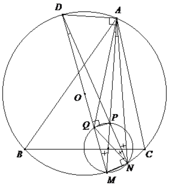
1). Vì MP là đường kính suy ra P N ⊥ M N (1).
Vì MD là đường kính suy ra D N ⊥ M N (2).
Từ (1) và (2), suy ra N; P; D thẳng hàng.

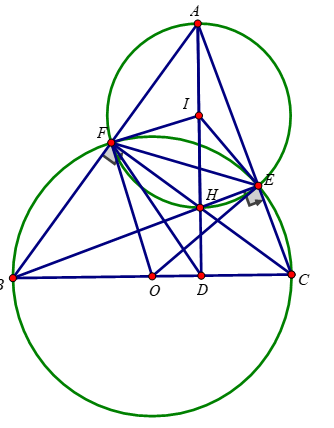
\(\text{a) Ta có:}\)
∠BFC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AFC = 90o
∠BEC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AEC = 90o
Tứ giác AEHF có:
∠AFC = 90o
∠AEC = 90o
=>∠AFC + ∠AEC = 180o
=> AEHF là tứ giác nội tiếp
b) ∠AFH = 90o => AH là đường kính đường tròn ngoại tiếp tứ giác AEHF
\(\text{Do đó trung điểm I của AH là tâm đường tròn ngoại tiếp tứ giác AEHF}\)
=> Bán kính đường tròn ngoại tiếp tứ giác AEHF là R = AI = \(\frac{AH}{2}\) = 2cm
Ta có: ∠BAC = 60o
=> ∠FIE = 2∠BAC = 120o (Góc nội tiếp bằng \(\frac{1}{2}\) góc ở tâm cùng chắn một cung)
=> Số đo ∠EHF = 120o
Diện tích hình quạt IEHF là:
\(S=\frac{\pi R^2N}{360}=\frac{\pi.2^2.120}{360}=\frac{4\pi}{3}\left(ĐVDT\right)\)
\(\text{c) Xét tam giác ABC có: }\)
BE và CF là các đường cao
BE giao với CF tại H
=> H là trực tâm tam giác ABC
=>AH ⊥ BC hay ∠ADC = ∠ADB = 90o
Xét tứ giác BEFC có:
∠BFC = ∠BEC = 90o
=> 2 đỉnh E, F cùng nhìn cạnh BC dưới 1 góc bằng nhau
=> BEFC là tứ giác nội tiếp
=> ∠HFE = ∠BEC ( 2 góc nội tiếp cùng chắn cung EC) (1)
Xét tứ giác BFHD có:
∠BFH = ∠HDB = 90o
=>∠BFH + ∠HDB = 180o
=> Tứ giác BFHD là tứ giác nội tiếp ( tổng 2 góc đối bằng 180o)
=> ∠DFH = ∠BEC ( 2 góc nội tiếp cùng chắn cung HD) (2)
Từ (1) và (2) = > ∠HFE = ∠DFH
=> FH tia phân giác của góc ∠DFE
d) Tam giác OFB cân tại O => ∠OFB = ∠FBO
Tam giác BFC vuông tại F => ∠FBO + ∠HCD = 90o
=> ∠OFB + ∠HCD = 90o (*)
\(\hept{\begin{cases}\Delta FIH\text{CÂN TẠI I}\\\widehat{IHF}=\widehat{DHC}\left(\text{ĐỐI ĐỈNH}\right)\\\Delta HDC\text{VUÔNG TẠI D}\Rightarrow\widehat{DHC}+\widehat{HDC}=90^0\end{cases}}\Rightarrow\widehat{IFH}+\widehat{HDC}=90^0\)
Từ (*) và (**) => ∠OFB = ∠IFH
=> ∠OFB + ∠OFH = ∠IFH + ∠OFH <=> ∠BFC = ∠FIO <=> ∠FIO) = 90o
Vậy FI là tiếp tuyến của (O)
Chứng minh tương tự EI là tiếp tuyến của (O)
Mà I là trung điểm của AH
=> Tiếp tuyến của (O) tại E và F và AH đồng quy tại 1 điểm.
HÌNH THÌ VÀO THỐNG KÊ HỎI ĐÁP CỦA MIK NHA
VCN JACK trả lời cuc64 kì đ luôn . đ là chất