Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

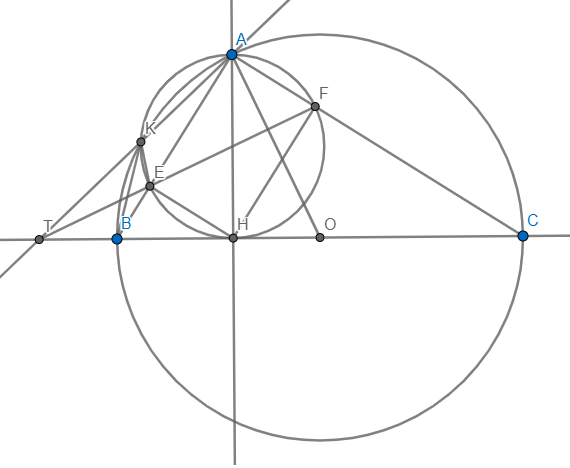
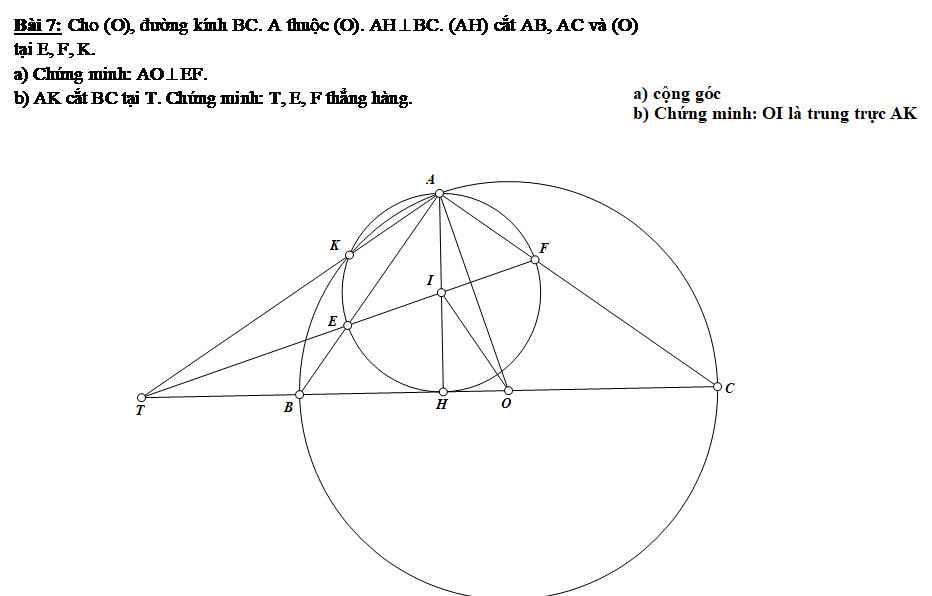
tứ giác BFEC có hai góc kề nhau cùng nhìn đoạn BC dưới một góc vuông : BFCˆ=BECˆ(=90)BFC^=BEC^(=90) ==> Tức giác BFEC là tứ giác nội tiếp
==> 4 điểm B,E,F,C cùng thuộc một đường tròn.

a) Vì AH là đường kính \(\Rightarrow\angle AEH=\angle AFH=90\)
Vì BC là đường kính \(\Rightarrow\angle BAC=90\Rightarrow\angle AEH=\angle AFH=\angle EAF=90\)
\(\Rightarrow AEHF\) là hình chữ nhật
\(\Rightarrow\angle AEF=\angle AHF=\angle ACH\left(=90-\angle HAC\right)\)
\(\Rightarrow\angle AEF+\angle ABC=\angle ACH+\angle ABC=90\)
mà \(\angle ABC=\angle BAO\) (\(\Delta ABO\) cân tại O)
\(\Rightarrow\angle AEF+\angle BAO=90\Rightarrow EF\bot AO\)
c) EF cắt BC tại T'.T'A cắt (O) tại K'
Vì \(\angle AEF=\angle ACH\Rightarrow EFCB\) nội tiếp
Xét \(\Delta T'EB\) và \(\Delta T'CF:\) Ta có: \(\left\{{}\begin{matrix}\angle T'EB=\angle T'CF\\\angle FT'Cchung\end{matrix}\right.\)
\(\Rightarrow\Delta T'EB\sim\Delta T'CF\left(g-g\right)\Rightarrow\dfrac{T'E}{T'C}=\dfrac{T'B}{T'F}\Rightarrow T'E.T'F=T'B.T'C\)
Vì AK'BC nội tiếp \(\Rightarrow\angle T'K'B=\angle T'CA\)
Xét \(\Delta T'K'B\) và \(\Delta T'CA:\) Ta có: \(\left\{{}\begin{matrix}\angle T'K'B=\angle T'CA\\\angle AT'Cchung\end{matrix}\right.\)
\(\Rightarrow\Delta T'K'B\sim\Delta T'CA\left(g-g\right)\Rightarrow\dfrac{T'K'}{T'C}=\dfrac{T'B}{T'A}\Rightarrow T'K'.T'A=T'B.T'C\)
\(\Rightarrow T'K'.T'A=T'E.T'F\Rightarrow\dfrac{T'K'}{T'F}=\dfrac{T'E}{T'A}\)
Xét \(\Delta T'EK'\) và \(\Delta T'AF:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{T'K'}{T'F}=\dfrac{T'E}{T'A}\\\angle FT'Achung\end{matrix}\right.\)
\(\Rightarrow\Delta T'EK'\sim\Delta T'AF\left(c-g-c\right)\Rightarrow\angle T'K'E=\angle T'FA\)
\(\Rightarrow AK'EF\) nội tiếp \(\Rightarrow K'\in\) đường tròn đường kính AH
\(\Rightarrow K'\equiv K\Rightarrow T'\equiv T\Rightarrow T,E,F\) thẳng hàng
a) AO cắt (O) tại F \(\Rightarrow AF\) là đường kính \(\Rightarrow\angle ADF=90\)
Vì DE là dây chung của (A;AH) và (O) và AO là đường nối tâm
\(\Rightarrow AO\bot DE\)
Xét \(\Delta ADK\) và \(\Delta AFD:\) Ta có: \(\left\{{}\begin{matrix}\angle DAFchung\\\angle AKD=\angle ADF=90\end{matrix}\right.\)
\(\Rightarrow\Delta ADK\sim\Delta AFD\left(g-g\right)\Rightarrow\dfrac{AD}{AF}=\dfrac{AK}{AD}\Rightarrow AD^2=AF.AK\)
mà \(AF=2AO\Rightarrow AD^2=2AO.AK\)
b) Xét \(\Delta AIK\) và \(\Delta AOH:\) Ta có: \(\left\{{}\begin{matrix}\angle HAOchung\\\angle AKI=\angle AHO=90\end{matrix}\right.\)
\(\Rightarrow\Delta AIK\sim\Delta AOH\left(g-g\right)\Rightarrow\dfrac{AI}{AO}=\dfrac{AK}{AH}\Rightarrow AI.AH=AK.AO\)
\(\Rightarrow AI.AH=\dfrac{AD^2}{2}=\dfrac{AH^2}{2}\) (cùng = bán kính của (A;AH))
\(\Rightarrow AI=\dfrac{AH}{2}\Rightarrow I\) là trung điểm AH