Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình như đề sai nha bạn
khi đó x + y + z = 1 ; x3 + y3 + z3 = 3
mà (x + y + z)3 = x3 + y3 + z3 + 3(x + y)(y + z)(z + x)
<=> 13 = 3 + 3(x + y)(y + z)(z + x)
<=> 3(x + y)(y + z)(z + x) = -2 (vô lý vì 3(x + y)(y + z)(z + x) > 0)
Iuukweewddukhkhuckekwhkuekcwuhwdikeuldkhscuhkjdcshudscjhukidschfshjrskdhjfursiuhukerfhevkhgyrukeaguukeeafduuhkafeuiehfugkurfrfaegukurgfeuwukfegukuqrfrekgquufrequgkuefqehhmeihuewkfkihurfewuhkifrekwhhubrhefjwkhjbkefeqhebfeqkehbfjkeahejchkeajhhkeceahjbkceeabhjrevahkbjreahhjvjbhkvfhhjkfvsrhhkjbhkrjfeahjhkvreajhbkvesrhvbjerahjbkrfeajhhkefrahhikferahhkjfreahhrfeajfrehuiqkrhehiakfhfhhrefkiuahiukrfea

Nửa chu vi của tấm bìa là: 80 : 2 = 40 (cm)
Gọi chiều rộng của tấm bìa là x (0 < x < 20, cm)
Chiều dài của tấm bìa là 40 – x (cm)
Cắt bỏ 4 góc của tấm bìa rồi gập lại thành dạng hình hộp khi đó:
Chiều dài của hình hộp là: 40 – x – 6 = 34 – x (cm)
Chiều rộng của hình hộp là x – 6 (cm)
Chiều cao của hình hộp là 3 cm
Lúc này diện tích hình hộp chữ nhật bằng 339 c m 2 và bằng tổng diện tích xung quanh với diện tích một đáy của nó
Ta có phương trình:
[(34 – x + x – 6).2].3 + (34 – x)(x – 6) = 339
↔ 28.2.3 + 34x – 204 – x 2 + 6x = 339
↔ 168 + 40x – 204 – x 2 = 339 ↔ x 2 – 40x + 375 = 0
∆’ = ( − 20 ) 2 – 1.375 = 25 > 0
Phương trình có hai nghiệm
x 1 = 20 + 25 = 25 k t m
hoặc x 2 = 20 - 25 = 15 t m
Vậy tấm bìa ban đầu có kích thước chiều rộng là 15cm và chiều dài là
40 – 15 = 25cm
Đáp án: D

Diện tích hình vuông cạnh c là \(S=c^2\)
Tổng diện tích hai hình chữ nhật là \(S_1=2ab\)
Xét tg vuông có \(c^2=a^2+b^2\)
Áp dụng cosi có
\(\frac{a+b}{2}\ge\sqrt{ab}\Rightarrow\frac{a^2+b^2+2ab}{4}\ge ab\Rightarrow a^2+b^2\ge2ab\) Dấu = xảy ra khi \(a=b\)
\(\Rightarrow S\ge S_1\left(dpcm\right)\)
\(S=S_1\) Khi a=b => tg ban đầu phải là tg vuông cân

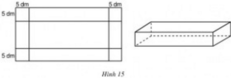
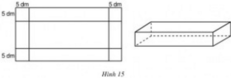
Gọi chiều rộng của miếng tôn là x(dm), x>10. Chiều dài của nó là 2x(dm).
Khi làm thành một cái thùng không đáy thì chiều dài của thùng là 2x-10(dm), chiều rộng là x-10 (dm), chiều cao laf5(dm).Dung tích của thùng là 5(2x-10)(x-10) d m 3
Theo đầu bài ta có phương trình:
5(2x-10)(x-10)=1500 hay x 2 - 15 x - 100 = 0
Giải phương trình: ∆ = 225 + 400 = 625 , ∆ = 25 ; x 1 = 20 , x 2 = - 5
Trả lời: Miếng tôn có chiều rộng bằng 20 (dm), chiều dài bằng 40(dm)

Bạn tự kết luận nhé.\(A=x\left(80-2x\right)\left(50-2x\right)=2x\left(40-x\right)\left(50-2x\right)=\dfrac{2}{3}.3x\left(40-x\right)\left(50-2x\right)\le\dfrac{2}{3}.\left[\dfrac{\left(3x\right)+\left(40-x\right)+\left(50-2x\right)}{3}\right]^3=\dfrac{2}{3}.\left(\dfrac{90}{3}\right)^3=18000\)Dấu "=" xảy ra \(\Leftrightarrow3x=40-x=50-2x\Leftrightarrow x=10\)
Vậy \(MaxA=18000\)
Ta sẽ tìm max của \(P=x\left(80-2x\right)\left(50-2x\right)\) với \(0< x< 25\).
Ta có:
\(P=x\left(80-2x\right)\left(50-2x\right)=\dfrac{2}{3}.3x.\left(40-x\right)\left(50-2x\right)\)
\(\le\dfrac{2}{3}\left(\dfrac{3x+40-x+50-2x}{3}\right)^3=\dfrac{2}{3}.\left(\dfrac{90}{3}\right)^3=18000\)
Dấu \(=\) xảy ra khi \(3x=40-x=50-2x\Leftrightarrow x=10\) (thỏa mãn)