Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sao bài của bạn giống bài mk thế nhỉ bài mk đăng đc 10' rùi!!! Giống hệt lun

\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)
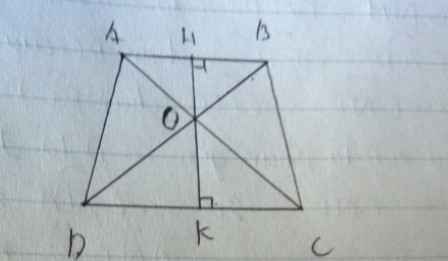
Kẻ hai đường cao DH,BK của hình thang ABCD(H\(\in\)AB, K\(\in\)DC)
Vì DH là đường cao của hình thang ABCD
nên \(S_{ABCD}=\dfrac{1}{2}\cdot DH\cdot\left(AB+CD\right)\left(1\right)\)
Vì BK là đường cao của hình thang ABCD
nên \(S_{ABCD}=\dfrac{1}{2}\cdot BK\cdot\left(AB+CD\right)\left(2\right)\)
Từ (1) và (2) suy ra DH=BK
Xét ΔADB có DH\(\perp\)AB tại H
nên \(S_{DAB}=\dfrac{1}{2}\cdot DH\cdot AB\)
Xét ΔBDC có BK là đường cao
nên \(S_{BDC}=\dfrac{1}{2}\cdot BK\cdot DC\)
=>\(\dfrac{S_{DAB}}{S_{BDC}}=\dfrac{\dfrac{1}{2}\cdot DH\cdot AB}{\dfrac{1}{2}\cdot BK\cdot DC}=\dfrac{AB}{DC}=\dfrac{2}{3}\)
=>\(S_{BDC}=\dfrac{3}{2}\cdot S_{DAB}\)
mà \(S_{BDC}+S_{DAB}=S_{ABCD}=95cm^2\)
nên \(S_{DAB}\left(1+\dfrac{3}{2}\right)=95\)
=>\(S_{DAB}\cdot\dfrac{5}{2}=95\)
=>\(S_{DAB}=38\left(cm^2\right)\)