Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(BCC'B'\) là hình chữ nhật \( \Rightarrow BC\parallel B'C'\)
\( \Rightarrow \left( {AB,B'C'} \right) = \left( {AB,BC} \right) = \widehat {ABC} = {60^ \circ }\).
b)
\(\Delta AA'B\) vuông tại \(A \Rightarrow \tan \widehat {ABA'} = \frac{{AA'}}{{AB}} = \frac{a}{a} = 1 \Rightarrow \widehat {ABA'} = {45^ \circ }\)
Vậy \(\left( {A'B,\left( {ABC} \right)} \right) = {45^ \circ }\).
c) \(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot BC,CC' \bot CM\)
Vậy \(\widehat {BCM}\) là góc nhị diện \(\left[ {B,CC',M} \right]\).
\(\Delta ABC\) đều \( \Rightarrow \widehat {BCM} = \frac{1}{2}\widehat {ACB} = {30^ \circ }\).
d) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right)\)
\(\Delta ABC\) đều \( \Rightarrow CM = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\).
\(\left. \begin{array}{l}CC'\parallel AA'\\AA' \subset \left( {ABB'A'} \right)\end{array} \right\} \Rightarrow CC'\parallel \left( {ABB'A'} \right)\)
\( \Rightarrow d\left( {CC',\left( {ABB'A'} \right)} \right) = d\left( {C,\left( {ABB'A'} \right)} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot CM\)
\(\Delta ABC\) đều \( \Rightarrow CM \bot AB\).
\( \Rightarrow CM \bot \left( {ABB'A'} \right) \Rightarrow CM \bot A'M\)
\(CC' \bot \left( {ABC} \right) \Rightarrow CC' \bot CM\)
\( \Rightarrow d\left( {CC',A'M} \right) = CM = \frac{{a\sqrt 3 }}{2}\)
g) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4},h = AA' = a\)
\( \Rightarrow {V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{{a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}\sqrt 3 }}{4}\)
\({S_{\Delta MBC}} = \frac{1}{2}{S_{\Delta ABC}} = \frac{{{a^2}\sqrt 3 }}{8},h = AA' = a\)
\( \Rightarrow {V_{A'.MBC}} = \frac{1}{3}{S_{\Delta MBC}}.AA' = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{8}.a = \frac{{{a^3}\sqrt 3 }}{{24}}\)

tham khảo
a) Vì \(AA'//BB'\) nên góc giữa \(AA'\) và \(BC\) là góc giữa \(BB'\) và \(BC\).
Vì cạnh bên vuông góc với đáy nên \(BB'\perp BC\). Do đó, \(\widehat{B'BC}=90^o\)
Vì \(A'B'//AB\) nên góc giữa \(A'B'\) và \(AC\) là góc giữa \(AB\) và \(AC\).
Ta có:\(\cos\widehat{BAC}=\dfrac{2,4^2+2,4^2-2^2}{2.2,4.2,4}=\dfrac{47}{72}\)
Nên \(\widehat{BAC}=49,2^o\)
b) Kẻ \(AH\perp BC\). Vì cạnh bên vuông góc với đáy nên \(BB'\perp AH\).
Ta có \(AH\perp BB',AH\perp BC\) nên \(AH\perp\left(BCC'B'\right)\).

Đáp án B.
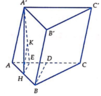
Do H là trung điểm AB nên
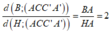
=> d(B;(ACC'A'))= 2d(H;(ACC'A'))
Ta có A'H ⊥ (ABC) nên
![]()
Gọi D là trung điểm của AC thì BD ⊥ AC
Kẻ HE
⊥
AC, ![]()
Ta có 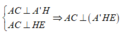
![]()
Trong (A'HE) kẻ HK
⊥
A'E, ![]()
Suy ra ![]()
![]() = 2HK
= 2HK
Ta có ![]()
![]()
Xét tam giác vuông A'AH có ![]()
Xét tam giác vuông A'HE có
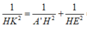
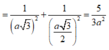
![]()
![]()

Đáp án D.

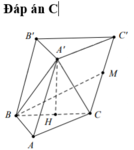
Nhận thấy ∆ ABC là hình chiếu của ∆ AMC' lên mặt phẳng (ABC).
Gọi φ là góc giữa (AMC') và (ABC)
![]()

Ta có 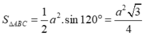
![]()
![]()
=> C'M = 2a

![]()
![]()
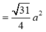
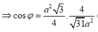
![]()

Gọi D là trung điểm AB \(\Rightarrow A'D\perp\left(ABC\right)\)
\(\Rightarrow CD\) là hình chiếu vuông góc của A'C lên (ABC)
\(\Rightarrow\widehat{A'CD}\) là góc giữa A'C và (ABC) \(\Rightarrow\widehat{A'CD}=60^0\)
\(CD=\dfrac{AB\sqrt{3}}{2}=a\sqrt{3}\) (trung tuyến tam giác đều)
\(\Rightarrow A'D=CD.tan60^0=3a\)
Từ D kẻ \(DE\perp AC\) (E thuộc AC)
Mà \(A'D\perp\left(ABC\right)\Rightarrow A'D\perp AC\)
\(\Rightarrow AC\perp\left(A'DE\right)\Rightarrow\widehat{AED}\) là góc giữa (A'AC) và (ABC)
\(DE=AD.sinA=a.sin60^0=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow A'E=\sqrt{A'D^2+DE^2}=\dfrac{a\sqrt{39}}{2}\)
\(\Rightarrow cos\widehat{A'ED}=\dfrac{DE}{A'E}=\dfrac{\sqrt{13}}{13}\)
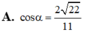
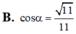
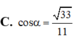
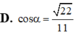
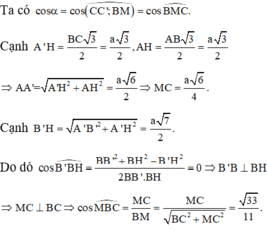
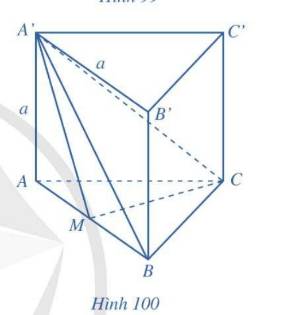


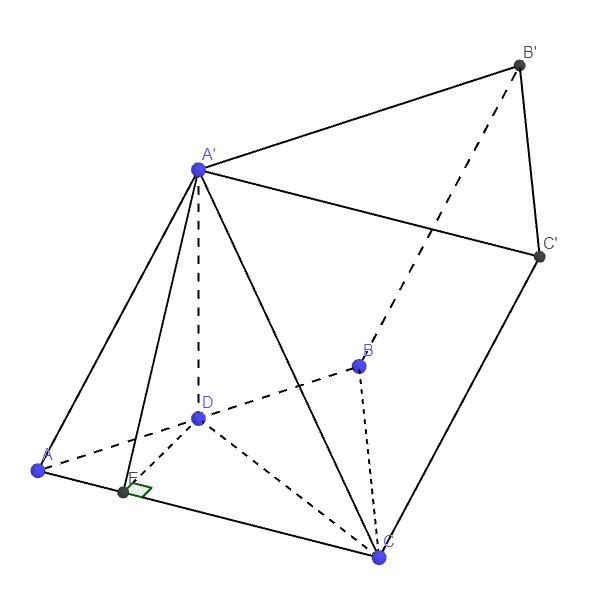
M là điểm nào thế bạn?
Akai Haruma
M là trung điểm AC ạ