

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a.
Do N là trọng tâm tam giác ABC \(\Rightarrow\) N là giao điểm AK và BO
Hay A,N,K,F thẳng hàng
\(\Rightarrow\left(AMN\right)\cap\left(SCD\right)=MF\)
b.
Trong mp (SCD) nối FM kéo dài cắt SD tại I
Dễ dàng nhận thấy \(SO=\left(SAC\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}M\in SC\in\left(SAC\right)\\M\in\left(AMN\right)\end{matrix}\right.\) \(\Rightarrow AM=\left(SAC\right)\cap\left(AMN\right)\)
\(N\in BD\in\left(SBD\right)\Rightarrow N\in\left(AMN\right)\cap\left(SBD\right)\)
\(\left\{{}\begin{matrix}I\in SD\in\left(SBD\right)\\I\in\left(AMN\right)\end{matrix}\right.\) \(\Rightarrow IN=\left(SBD\right)\cap\left(AMN\right)\)
\(\Rightarrow\) 3 mặt phẳng (AMN), (SAC), (SBD) cắt nhau theo 3 giao tuyến phân biệt SO, AM, IN nên 3 đường thẳng này song song hoặc đồng quy
Mà SO cắt AM tại E \(\Rightarrow SO;AM;NI\) đồng quy tại E
Hay N;E;I thẳng hàng
M là trung điểm SC, O là trung điểm AC \(\Rightarrow\) E là trọng tâm tam giác SAC
\(\Rightarrow\dfrac{OE}{OS}=\dfrac{1}{3}\)
Theo giả thiết N là trọng tâm ABC \(\Rightarrow\dfrac{ON}{OB}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{OE}{OS}=\dfrac{ON}{OB}\Rightarrow EN||SB\Rightarrow NI||SB\Rightarrow NI||\left(SBC\right)\)
c.
Do \(CF||AB\), áp dụng định lý Talet:
\(\dfrac{KF}{AK}=\dfrac{KC}{KB}=1\Rightarrow KF=AK\)
Do \(AD||BK\) \(\Rightarrow\dfrac{KN}{AN}=\dfrac{BK}{AD}=\dfrac{1}{2}\Rightarrow KN=\dfrac{1}{2}AN\)
\(\Rightarrow KN=\dfrac{1}{2}\left(AK-KN\right)\Rightarrow KN=\dfrac{1}{3}AK=\dfrac{1}{3}KF\)
\(\Rightarrow KF=3KN=3\left(NF-KF\right)\)
\(\Rightarrow KF=\dfrac{3}{4}NF\)
Theo giả thiết M, K lần lượt là trung điểm SC, BC \(\Rightarrow MK\) là đường trung bình tam giác SBC
\(\Rightarrow MK||SB\Rightarrow MK||IN\) (theo c/m câu b)
Áp dụng định lý Talet:
\(\dfrac{KM}{IN}=\dfrac{KF}{NF}=\dfrac{3}{4}\Rightarrow KM=\dfrac{3}{4}IN\)
\(\Rightarrow d\left(M;AF\right)=\dfrac{3}{4}d\left(I;AF\right)\)
\(\Rightarrow\dfrac{S_{\Delta FKM}}{S_{\Delta KAI}}=\dfrac{\dfrac{1}{2}.d\left(M;KF\right).KF}{\dfrac{1}{2}d\left(I;AK\right).AK}=\dfrac{3}{4}.1=\dfrac{3}{4}\)

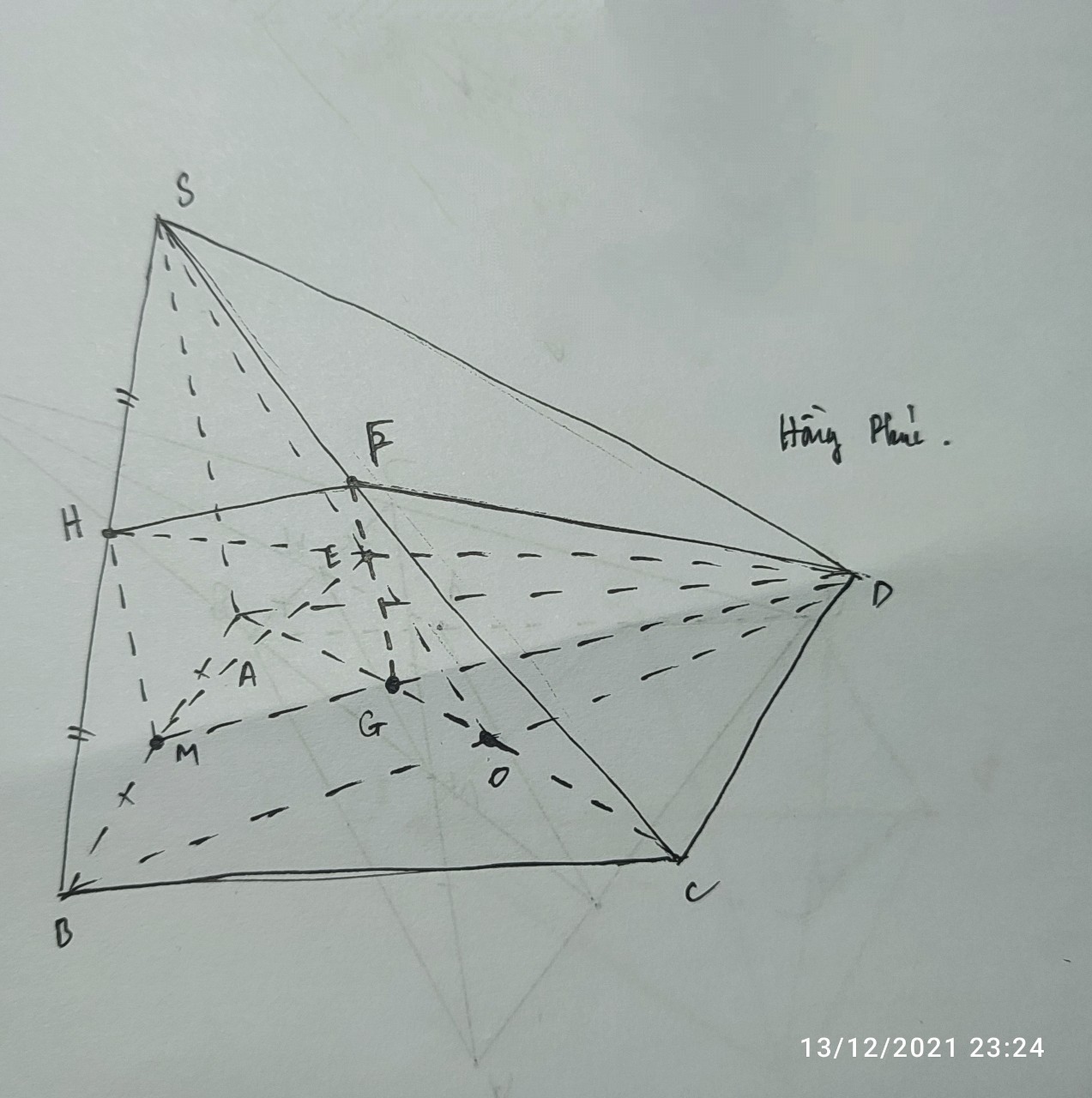
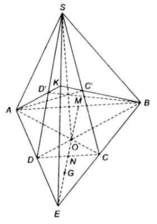
Hình câu c là tui vẽ riêng ra cho dễ nhìn thôi, còn hình vẽ trình bày vô bài lấy hình chung ở câu a và b nhó :v



a) Gọi N là giao điểm của EM và CD
Vì M là trung điểm của AB nên N là trung điểm của CD (do ABCD là hình thang)
⇒ EN đi qua G
⇒ S, E, M, G ∈ (α) = (SEM)
Gọi O là giao điểm của AC và BD
Ta có (α) ∩ (SAC) = SO
và (α) ∩ (SBD) = SO = d
b) Ta có: (SAD) ∩ (SBC) = SE
c) Gọi O' = AC' ∩ BD'
Ta có AC' ⊂ (SAC), BD' ⊂ (SBD)
⇒ O' ∈ SO = d = (SAC) ∩ (SBD)

\(SM=MA=SA-SM\Rightarrow SM=\dfrac{1}{2}SA\)
Do IM song song SO, áp dụng định lý Talet trong tam giác SAO:
\(\dfrac{IO}{OA}=\dfrac{SM}{SA}=\dfrac{1}{2}\)
Do NK song song SO, áp dụng định lý Talet cho tam giác SCO:
\(\dfrac{OK}{OC}=\dfrac{SN}{SC}=\dfrac{1}{3}\)
Mà ABCD là hình bình hành nên \(OA=OC\)
\(\Rightarrow\dfrac{OI}{OK}=\dfrac{3}{2}\)

a: Xét ΔSAC có
H,K lần lượt là trung điểm của SA,SC
=>HK là đường trung bình
=>HK//AC
Xét (GHK) và (ABCD) có
HK//AC
\(G\in\left(GHK\right)\cap\left(ABCD\right)\)
Do đó: (GHK) giao (ABCD)=xy, xy đi qua G và xy//HK//AC
b: Chọn mp(SBD) có chứa SD
Gọi O là giao điểm của AC và BD
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔABC có
G là trọng tâm
BO là trung tuyến của ΔABC
Do đó: B,O,G thẳng hàng
=>G\(\in\)BD
Trong mp(SAC), gọi I là giao điểm của SO với HK
\(I\in SO\subset\left(SBD\right);I\in HK\subset\left(GHK\right)\)
=>\(I\in\left(SBD\right)\cap\left(GHK\right)\)(1)
\(G\in BD\subset\left(SBD\right);G\in\left(GHK\right)\)
=>\(G\in\left(SBD\right)\cap\left(GHK\right)\left(2\right)\)
Từ (1) và (2) suy ra \(\left(SBD\right)\cap\left(GHK\right)=GI\)
Gọi M là giao điểm của SD với GI
=>M là giao điểm của SD với (SHK)
c: Xét ΔSAC có
O,K lần lượt là trung điểm của CA,CS
=>OK là đường trung bình của ΔSAC
=>OK//SA và OK=SA/2
OK=SA/2
SH=SA/2
Do đó: OK=SH
Xét tứ giác SHOK có
SH//OK
SH=OK
Do đó: SHOK là hình bình hành
=>HK cắt SO tại trung điểm của mỗi đường
mà E là trung điểm của HK
nên Elà trung điểm của SO
=>E trùng với I
=>(SBD) giao (GHK)=GE
=>G,E,M thẳng hàng