K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
17 tháng 12 2018
Chọn A
Dựa vào đồ thị, ta có
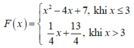
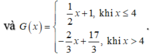
Khi đó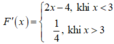 
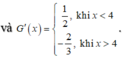
Ta có P(x) = F(x)G(x) 
Do đó 
23 tháng 5 2017
a) Ta có tập xác định của cả hai hàm số \(f\left(x\right),g\left(x\right)\) đểu là \(\mathbb{R}\)
Mặt khác:
\(f\left(-x\right)=\dfrac{a^{-x}+a^{-x}}{2}=f\left(x\right);g\left(x\right)=\dfrac{a^{-x}-a^x}{2}=-g\left(x\right)\)
Vậy \(f\left(x\right)\) là hàm số chẵn, \(g\left(x\right)\) làm hàm số lẻ
b) Ta có :
\(f\left(x\right)=\dfrac{a^x+a^{-x}}{2}\ge\sqrt{a^xa^{-x}}=1,\forall x\in\mathbb{R}\)
và :
\(f\left(0\right)=\dfrac{a^0+a^0}{2}=1\)
Vậy :
\(minf\left(x\right)=f\left(0\right)=1\)
CM
16 tháng 8 2019
| ∫ P(x) e x dx | ∫ P(x)cosxdx | ∫ P(x)lnxdx |
| P(x) | P(x) | P(x)lnx |
| e x dx | cosxdx | dx |
TH
1
K
1 tháng 8 2020
\(y'=\frac{\left(\frac{x+1}{-x+1}\right)}{1+\left(\frac{x+1}{-x+1}\right)^2}-\frac{1}{1+x^2}=\frac{2}{\left(1-x\right)^2}.\frac{\left(1-x\right)^2}{\left(1-x\right)^2+\left(x+1\right)^2}-\frac{1}{1+x^2}\)\(=\frac{2}{2\left(1+x^2\right)}-\frac{1}{1+x^2}=0;\forall x\ne1\)
- Xét \(x\in\left(-\infty,1\right):y'=0,\forall x\in\left(-\infty,1\right)\)nên y là hằng số trên \(\left(-\infty,1\right)\)
mà \(y\left(0\right)=arctg1-arctg0=\frac{\eta}{4}-0=\frac{\eta}{4}\Rightarrow y=\frac{\eta}{4},\forall x\in\left(-\infty,1\right)\)(n số pi ở đây không chắc là đúng chưa mình mở vô hộp có kí tự số pi rồi mà thấy kí tự có hơi lạ lạ, thông cảm nhá)
- Xét \(x\in\left(1,\infty\right):y'=0,\forall x\in\left(1,\infty\right)\)
\(\Rightarrow y\)là hằng số trên \(\left(1,\infty\right)\)
\(\Rightarrow arctg\left(\frac{1+x}{1-x}\right)-arctgx=k,\forall x\in\left(1,\infty\right)\)
Cho \(x\rightarrow\infty\)thì \(\left(\frac{1+x}{1-x}\right)\rightarrow-1:arctg\left(-1\right)-\frac{\eta}{2}=k\Rightarrow k=-\frac{\eta}{4}-\frac{\eta}{2}=-\frac{3\eta}{4}\)
Do đó \(y=-\frac{3\eta}{4},\forall x\in\left(1,\infty\right).\)
Vậy \(y=\hept{\begin{cases}\frac{\eta}{4}\left(neux< 1\right)\\-\frac{3\eta}{4}\left(neux>1\right)\end{cases}}\)nếu đó nha.
CM
24 tháng 1 2019
Chọn A.
(P1): y = f(x) = 1 4 x 2 - x có đỉnh I 2 (2;-1)
P(2): y = g(x) =
a
x
2
-
4
a
x
+
b
(a>0) 
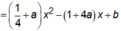
Duy ra I1, I2, I cùng nằm trên đường thẳng x = 2.
Mà giao điểm của (P1) và Ox là A(4;0) và B(0;0).
Suy ra tứ giác lồi AI1BI2 có hai đường chéo vuông góc và b – 4a >0
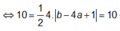
Tam giác IAB có diện tích là
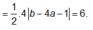
8.481.916.196.482 nha