Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy r = và đường cao h = r, đwòng sinh l = a.
Vậy Sxq = πrl = ( đơn vị diện tích)
Sđáy = =
( đơn vị diện tích);
Vnón =
( đơn vị thể tích)
b) Gọi tâm đáy là O và trung điểm cạnh BC là I.
Theo giả thiết, = 600.
Ta có diện tích ∆ SBC là: S = (SI.BC)/2
Ta có SO + SI.sin600 = .
Vậy .
Ta có ∆ OIB vuông ở I và BO = r = ;
OI = SI.cos600 = .
Vậy BI = và BC =
.
Do đó S = (SI.BC)/2 = (đơn vị diện tích)

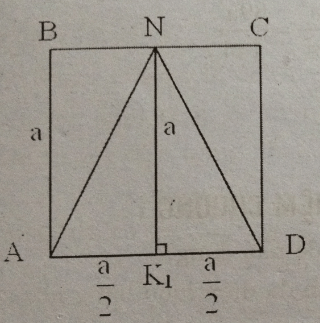
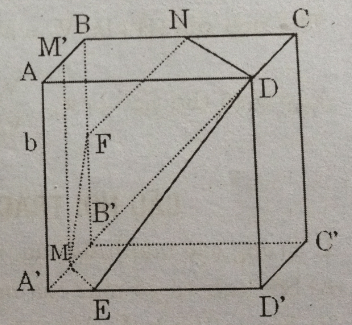
b)-Mặt phẳng (DMN) cắt hình lập phương theo thiết diện MEDNF trong đó ME // ND, FN //DE và chia hình lập phương thành hai khối đa diện (H) và (H’), gọi phần khối lập phương chứa A, B, A’, mặt phẳng (DMN) là (H)
-Chia (H) thành các hình chóp F.DBN, D.ABFMA’ và D.A’EM.

A E M B C H N S
Xét tam giác ABC có : \(BC=AB.\tan60^0=2a\sqrt{3}\Rightarrow S_{\Delta ABC}=2a^2\sqrt{3}\)
\(V_{S.ABCD}=\frac{1}{3}SA.S_{\Delta ABC}=\frac{1}{3}a\sqrt{3}.2a^2\sqrt{3}=2a^3\)
- Gọi N là trung điểm cạnh SA. Do SB//(CMN) nên d(SB. CM)=d(SB,(CMN))
=d(B,(CMN))
=d(A,(CMN))
- Kẻ \(AE\perp MC,E\in MC\) và kẻ \(AH\perp NE,H\in NE\), ta chứng minh được \(AH\perp\left(CMN\right)\Rightarrow d\left(A,\left(CMN\right)\right)=AH\)
Tính \(AE=\frac{2S_{\Delta AMC}}{MC}\) trong đó :
\(S_{\Delta AMC}=\frac{1}{2}AM.AC.\sin\widehat{CAM}=\frac{1}{2}a.4a\frac{\sqrt{3}}{2}=a^2\sqrt{3};MC=a\sqrt{13}\)
\(\Rightarrow AE=\frac{2a\sqrt{3}}{\sqrt{13}}\)
Tính được \(AH=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(A,\left(CMN\right)\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\Rightarrow d\left(SB,CM\right)=\frac{2a\sqrt{3}}{\sqrt{29}}\)

Dễ dàng chứng minh MN // BC
Xét \(\Delta SBC\) có MN // BC và MN đi qua trọng tâm G
\(\Rightarrow\) \(\begin{cases}SM=\frac{2}{3}SB\\SN=\frac{2}{3}SC\end{cases}\)
Sử dụng công thức tỉ lệ thể tích đố với 2 khối tứ diện S.AMN và S.ABC ta có
\(\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}=1.\frac{2}{3}.\frac{2}{3}=\frac{4}{9}\\ \Rightarrow V_{S.AMN}=\frac{4}{9}.V_{S.ABC}\)
Tính được \(V_{S.ABC}=\frac{1}{6}SA.AB.BC=\frac{a^3}{6}\)
\(\Rightarrow V_{S.AMN}=\frac{2a^3}{27}\)



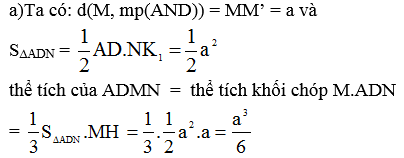


19.
Giống câu 6?
20.
\(\int\frac{x+1}{2x+1}dx=\frac{1}{2}\int\left(1+\frac{1}{2x+1}\right)dx=\frac{1}{2}x+\frac{1}{4}ln\left(2x+1\right)+C\)
21.
\(S=\frac{\left(2a\right)^2\sqrt{3}}{4}=a^2\sqrt{3}\)
\(\Rightarrow V=S.AA'=3a^3\)
16.
\(log_4\left(ab\right)=log_4\left(ab^4\right)\)
\(\Leftrightarrow log_4a+log_4b=log_4a+log_4b^4\)
\(\Leftrightarrow log_4b=log_4b^4\)
\(\Rightarrow b=1\)
Ủa hình như bạn ghi ko đúng đề, ko liên quan gì đáp án hết
17.
\(\left(\frac{4}{3}\right)^{3x+4}\le\left(\frac{4}{3}\right)^{3x^2+4x}\)
\(\Leftrightarrow3x+4\le3x^2+4x\) (do \(\frac{4}{3}>1\))
\(\Leftrightarrow3x^2+x-4\ge0\Rightarrow\left[{}\begin{matrix}x\le-\frac{4}{3}\\x\ge1\end{matrix}\right.\)
\(D=(-\infty;-\frac{4}{3}]\cup[1;+\infty)\)
18.
\(h=R\sqrt{3}\Rightarrow R=\frac{h}{\sqrt{3}}=\frac{4}{\sqrt{3}}\)
\(\Rightarrow V=\frac{1}{3}\pi R^2h=\frac{64\pi}{9}\)