


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




1). Tam giác ABF và tam giác ACE ần lượt cân tại F, E và
F B A ^ = E C A ^ = A ^ 2 ⇒ Δ A B F ∽ Δ A C E .
2). Giả sử G là giao điểm của BE và CF.
Ta có G F G C = B F C E = A B A C = D B D C ⇒ G D ∥ F B , và F B ∥ A D ta có G ∈ A D .
3). Chứng minh B Q G ^ = Q G A ^ = G A E ^ = G A C ^ + C A E ^ = G A B ^ + B A F ^ = G A F ^ , nên AGQF nội tiếp, và Q P G ^ = G C E ^ = G F Q ^ , suy ra tứ giác FQGP nội tiếp.
1) Chứng minh rằng tam giác \( A B F \) đồng dạng với tam giác \( A C E \):
- Tam giác \(ABF\) và \(ACE\) có:
+ Góc \(A\) chung.
+ Góc \(BAF\) bằng góc \(CAE\) (vì \(AD\) là phân giác của góc \(BAC\) và \(CF\), \(BE\) song song với \(AD\)).
Do đó, tam giác \(ABF\) đồng dạng với tam giác \(ACE\) (theo trường hợp góc-góc).
2) Chứng minh rằng các đường thẳng \(BE\), \(CF\), \(AD\) đồng quy:
- Gọi \(G\) là giao điểm của \(BE\) và \(CF\).
- \(AD\) là phân giác góc \(BAC\), và \(BE\), \(CF\) song song với \(AD\). Do đó, \(G\) cũng nằm trên phân giác \(AD\).
- Vậy \(BE\), \(CF\), \(AD\) đồng quy tại \(G\).
3) Chứng minh rằng các điểm \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn:
- Gọi đường tròn ngoại tiếp tam giác \(GEC\) là \(\omega\).
- \(QE\) cắt \(\omega\) tại \(P\) khác \(E\), vậy \(P\) nằm trên đường tròn \(\omega\).
- \(GQ\) song song với \(AE\), và \(AE\) là đường kính của \(\omega\) (vì \(E\) là trung điểm của \(AC\) và \(G\) nằm trên phân giác của \(BAC\)). Do đó, \(GQ\) là dây cung của \(\omega\).
- \(PF\) là tiếp tuyến của \(\omega\) tại \(P\) (vì \(QE\) là tiếp tuyến và \(PF\) là phần kéo dài của \(QE\)).
- Góc \(PGF\) bằng góc \(GAC\) (cùng chắn cung \(GC\) của \(\omega\)).
- \(AF\) là trung trực của \(AB\), nên \(ABF\) là tam giác cân tại \(A\). Do đó, góc \(AFB\) bằng góc \(ABF\).
- Góc \(ABF\) bằng góc \(GAC\) (do đồng dạng của tam giác \(ABF\) và \(ACE\)).
- Vậy, góc \(PGF\) bằng góc \(AFB\). Do đó, \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn.


2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .

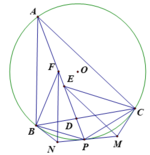
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.

\(\text{a) Xét tứ giác BEFC có:}\)
\(\text{∠BEC = 90 o (CE là đường cao)}\)
\(\text{∠BFC = 90 ^0 (BF là đường cao)}\)
=> 2 đỉnh E, F cùng nhìn cạnh BC dưới 1 góc vuông
=> Tứ giác BEFC là tứ giác nội tiếp
\(\text{Xét tứ giác AEHF có:}\)
\(\text{∠AEH = 90 o (CE là đường cao)}\)
\(\text{∠AFH = 90 o (BF là đường cao)}\)
=> ∠AEH + ∠AFH = 180^ o
=> Tứ giác AEHF là tứ giác nội tiếp.
\(\text{b) Xét ΔSBE và ΔSFC có:}\)
\(\text{∠FSC là góc chung}\)
\(\text{∠SEB = ∠SCF (Tứ giác BEFC là tứ giác nội tiếp)}\)
=> ΔSBE ∼ ΔSFC (g.g)
\(\Rightarrow\frac{SB}{SF}\)=\(\frac{SE}{SC}\)\(\Rightarrow\text{SE.SF = SB.SC (1)}\)
\(\text{Xét ΔSMC và ΔSNB có:}\)
\(\text{∠ NSC là góc chung}\)
\(\text{∠ SCM = ∠SNB (Hai góc nội tiếp cùng chắn cung MB)}\)
=> ΔSMC ∼ ΔSBN (g.g)
\(\Rightarrow\frac{SM}{SB}\)=\(\frac{SC}{SN}\Rightarrow\text{SM.SN = SB.SC (2)}\)
Từ (1) và (2) => SE.SF = SM.SN
\(\text{c) Ta có:}\)
\(\hept{\begin{cases}\widehat{KAE}=\widehat{KCB}\left(\text{2 GÓC NỘI TIẾP CÙNG CHẮN CUNG KB}\right)\\\widehat{HAE}=\widehat{BFM}\left(\text{TỨ GIÁC AEHF LÀ TỨ GIÁC NỘI TIẾP}\right)\\\widehat{KCB}=\widehat{BFM}\left(\text{TỨ GIÁC BEFC LÀ TỨ GIÁC NỘI TIẾP}\right)\end{cases}}\)
=> ∠KAE = ∠HAE
=> AE là tia phân giác của góc ∠KAH
\(\text{Mà AE cũng là đường cao của tam giác KAH}\)
=> ΔKAH cân tại A
=> AE là đường trung tuyến của ΔKAH
=> E là trung điểm của KH hay K và H đối xứng nhau qua AB
\(\text{d) Tia BF cắt đường tròn (O) tại J}\)
∠KJB = ∠KCB (2 góc nội tiếp cùng chắn cung KB)
∠KCB = ∠EFH (tứ giác BEFC là tứ giác nội tiếp )
=> ∠KJB = ∠EFH
Mà 2 góc này ở vị trí so le trong
=> KJ // EF
KI // EF (gt)
=> I ≡ J
=> H, F, J thẳng hàng
HÌNH THÌ VÀO XEM THỐNG KÊ HỎI ĐÁP NHA
BÀI LÀM ĐÚNG MÀ SAO CÓ NGƯỜI K SAI TÔI ĐẢM BẢO BÀI NÀY ĐÚNG 100%

a)Xét tam giác ACD và tam giác ECD(đều là vuông)![]()
ECD=DCA(Vì CD là p/giác)
CD là cạnh chung
\(\Rightarrow\)tam giác ACD=tam giác ECD(cạnh huyền góc nhọn)
b)Vì tam giác ACD=tam giác ECD(cạnh huyền góc nhọn)
\(\Rightarrow\)AD=DE(cạnh cặp tương ứng)
\(\Rightarrow\)D cách đều hai mút của AE
\(\Rightarrow\)CD là đường trung trực của AE
Do đó CI\(\perp\)AE
\(\Rightarrow\)Tam giác CIE là tam giác vuông
c)Vì AD=DE(câu b)
Mà tam giác BDE là tam giác vuông(tại E)
\(\Rightarrow\)DE<BD(cạnh góc vuông nhỏ hơn cạnh huyền)
\(\Rightarrow\)AD<BD(đpcm)
d)Kéo dài BK cắt AC tại O
Vì BK\(\perp\)CD(gt)
\(\Rightarrow\)CK là đường cao thứ nhất của tam giác OBC(1)
Vì tam giác ABC vuông tại A
Nên BA\(\perp\)AC
\(\Rightarrow\)BA là đường cao thứ hai của tam giác OBC(2)
Theo đề bài ta có DE\(\perp\)BC
Nên DE là đường cao thứ ba của tam giác OBC(3)
Từ (1),(2) và (3) suy ra:
Ba đường cao giao nhau tại một điểm trùng với điểm D
\(\Rightarrow\) 3 đường thẳng AC;DE;BK đồng quy(đpcm)

A B C I S D E F G K L K' M x
Gọi giao điểm khác D của hai đường tròn (BED);(CFD) là K'; K'I cắt EF tại L; DL cắt (I;ID) tại M khác D.
Ta thấy IE = IF; AI là phân giác ngoài của ^EAF, từ đây dễ suy ra 4 điểm A,E,I,F cùng thuộc một đường tròn
Vì 3 điểm D,F,E lần lượt thuộc các cạnh BC,CA,AB của \(\Delta\)ABC nên (BED);(CFD);(AFE) đồng quy (ĐL Miquel)
Hay điểm K' thuộc đường tròn (AIFE). Do vậy LI.LK' = LE.LF = LD.LM (= PL/(G) = PL/(I) )
Suy ra 4 điểm K',M,I,D cùng thuộc một đường tròn. Mà ID = IM nên ^IK'D = ^IK'M.
Đồng thời ^DIM = 1800 - ^DK'M = 1800 - ^EK'F + 2.^FK'D = ^BAC + 2.^ACB = 2.^AID
Suy ra IA vuông góc DM, từ đó M,L,D,A thẳng hàng (Vì IA cũng vuông góc AD)
Khi đó dễ thấy AL là phân giác ^BAC, K'L là phân giác ^EK'F, mà tứ giác AEK'F nội tiếp
Suy ra AEK'F là tứ giác điều hòa, từ đây AK' là đường đối trung của \(\Delta\)AEF
Suy ra K' trùng K. Kẻ tiếp tuyến Kx của (G), ta có ^BKx = ^EKx - ^EKB = ^EFK - ^EFD = ^BCK
Do đó (BKC) tiếp xúc với (G) tại K, tức KG đi qua tâm của (BKC) (1)
Gọi S là trung điểm cung lớn BC của (ABC). Có SB = SC và ^BKC = ^AED + ^AFD = 1800 - ^BSC/2
Suy ra S là tâm của đường tròn (BKC) (2)
Từ (1) và (2) suy ra KG luôn đi qua S cố định (Vì S là trung điểm cùng BC lớn cố định) (đpcm).

De chung minh M la tam duong tron bang tiep goc C cua tam giac ABC
\(\Rightarrow\widehat{MAI}=\widehat{MBI}=90^0\) => tu giac MAIN noi tiep
=> \(C'I.C'M=C'B.C'A\left(1\right)\)
Mat khac xet (O) ta cung co \(C'B.C'A=C'N.C'E\left(2\right)\)
Tu (1) va (2) suy ra \(C'I.C'M=C'E.C'N\)
suy ra tu giac MEIN noi tiep (*)
chung minh tuong tu cung co tu giac EINK noi tiep (**)
tu (*) va(**) ta co dpcm