Chu kì \(T=4s\Rightarrow\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{4}=\dfrac{\pi}{2}\)

Trong \(t=6s=T+\dfrac{T}{2}\)

Mà quãng đường đi được sau 6s là 48cm nên:

\(S=4A+2A=6A=48\Rightarrow A=8cm\)

Khi \(t=0\) vật qua VTCB và hướng về vị trí biên âm nên \(\varphi_0=\dfrac{\pi}{2}\).

PT dao động: 

\(x=Acos\left(\omega t+\varphi_0\right)=8cos\left(\dfrac{\pi}{2}t+\dfrac{\pi}{2}\right)\left(cm\right)\)

  

 

 

E = a+1/a-1 = a-1+2/a-1

= 1 +  2/a-1

Để E nguyên => 2/a-1 nguyên

Hay 2 chia hết cho (a-1)

=> a - 1 thuộc Ư(2)={±1;±2}

=> a thuộc { 2;0;3;-1}

\(E=\dfrac{a+1}{a-1}=\dfrac{a-1+2}{a-1}=1+\dfrac{2}{a-1}\)

\(E\in Z\Rightarrow2⋮\left(a-1\right)\)

\(\Rightarrow\left(a-1\right)\inƯ\left(2\right)\)

\(\Rightarrow\left(a-1\right)\in\left\{-1;1;-2;2\right\}\) và \(a\in Z\)

\(\Rightarrow a=\left\{0;2;-1;3\right\}\)

Trung bình (TB) là một khái niệm dùng để chỉ giá trị trung bình của một tập hợp các số hoặc giá trị. Mô (mô-ta) là một đơn vị cấu tạo cơ bản của cơ thể, chẳng hạn như tế bào, mô liên kết, mô cơ, mô thần kinh, vv. Cơ quan là một phần cấu thành của cơ thể, có chức năng cụ thể và thường được hình thành từ nhiều mô khác nhau. Hệ cơ quan là sự kết hợp của các cơ quan có chức năng tương đồng hoặc liên quan nhau, ví dụ như hệ tiêu hóa, hệ tuần hoàn, hệ thần kinh, vv. Cơ thể là tổng thể của tất cả các cơ quan, hệ cơ quan và mô trong cơ thể. Ví dụ minh họa trong thực tế: Hệ tiêu hóa trong cơ thể người. Hệ tiêu hóa bao gồm các cơ quan như dạ dày, ruột non, ruột già, gan, vv. Mỗi cơ quan này được hình thành từ các mô khác nhau như mô cơ, mô liên kết, mô tuyến, vv. Các cơ quan này hoạt động cùng nhau để tiếp nhận, xử lý và hấp thụ thức ăn, đồng thời loại bỏ chất thải. Trung bình (TB) có thể được sử dụng để tính toán lượng thức ăn trung bình mà hệ tiêu hóa cần tiêu thụ hàng ngày để duy trì sức khỏe. ...  

 Từ pt \(v=16\pi\cos\left(4\pi t-\dfrac{\pi}{6}\right)=16\pi\cos\left(4\pi t-\dfrac{2\pi}{3}+\dfrac{\pi}{2}\right)\) (cm/s), ta suy ra \(\omega=4\pi\left(rad/s\right)\), lại có \(\omega A=16\pi\Leftrightarrow A=\dfrac{16\pi}{\omega}=4\left(cm\right)\)

 \(\varphi_0=-\dfrac{2\pi}{3}\); \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)

 Đường tròn lượng giác: 

 

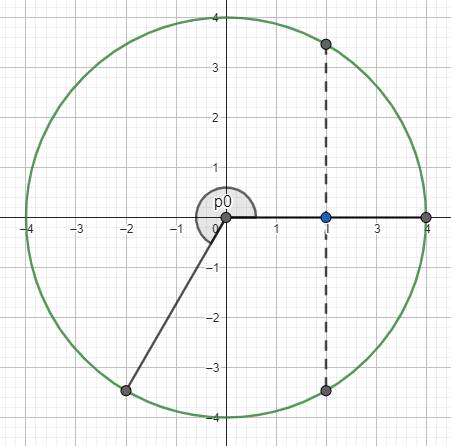
 Từ đây, ta có thể thấy tại thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ khi dao động, góc quét của vật là \(\Delta\varphi=\dfrac{\pi}{3}+1011.2\pi=\dfrac{6067}{3}\pi\) (rad)

 Thời điểm lần thứ 2023 vật chuyển động qua vị trí \(x=2\) kể từ lúc bắt đầu dao động là \(\Delta t=\dfrac{\Delta\varphi}{2\pi}.T=\dfrac{\dfrac{6067}{3}\pi}{2\pi}.0,5=\dfrac{6067}{12}\approx505,58\left(s\right)\)

a)Thời gian quả bóng rơi: \(t=\sqrt{\dfrac{2S}{g}}=\sqrt{\dfrac{2\cdot1,2}{9,81}}=0,5s\)

Tốc độ bóng ngay trước khi chạm đất: \(v=g\cdot t=9,81\cdot0,5=4,905m/s\)

b)Quãng đường vật rơi trong giây cuối cùng: 

\(\Delta S=1,2-S_1\)

Lí giải: Thời gian cả quá trình rơi \(t=0,5s\) thì thời gian đã đi trong giây đầu tiên không có nên câu b đề bài chưa hợp lí lắm.

Gọi quãng đường là: a (a>0)

Theo bài ra, ta có:

\(\dfrac{a}{10}+\dfrac{a}{15}=2\)

\(\Leftrightarrow\dfrac{5a}{30}=2\)

\(\Leftrightarrow5a=60\)

\(\Leftrightarrow a=12\)

Vậy quãng đường là 12km

Thời gian đi từ nhà đến trường là: \(t_1=\dfrac{s}{v_1}=\dfrac{s}{10}\left(h\right)\)

Thời gian đi từ trường về nhà là: \(t_2=\dfrac{s}{v_2}=\dfrac{s}{15}\left(h\right)\)

Tổng thời gian đi vế là 2h nên ta có: \(t_1+t_2=2\)

\(\Rightarrow\dfrac{s}{10}+\dfrac{s}{15}=2\)

\(\Rightarrow\dfrac{3s}{30}+\dfrac{2s}{30}=\dfrac{60}{30}\)

\(\Rightarrow\dfrac{5s}{30}=\dfrac{60}{30}\)

\(\Rightarrow5s=60\)

\(\Rightarrow s=\dfrac{60}{5}\)

\(\Rightarrow s=12\left(km\right)\)

Vậy quãng đường từ nhà đến trường là 12km 

Dao động điều hòa có nhiều lắm em, em cần cụ thể phần nào vậy???

a)Phương trình dao động điều hòa: \(m*a+k*x=0\)

với \(x\) là vị trí của con lắc lò xo treo.

b)\(F_{đh}=-k\cdot x=-100\cdot0,01=-1N\)

c)\(F_{đhmin}=-100\cdot0,03=-3N\)

\(F_{đhmax}=100\cdot0,03=3N\)

d)Chu kì: \(T=2\pi\cdot\sqrt{\dfrac{m}{k}}=2\pi\cdot\sqrt{\dfrac{0,1}{100}}\left(s\right)\)

\(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{2\pi\cdot\sqrt{\dfrac{0,1}{100}}}\)

Thời gian ngắn nhất: \(t=\dfrac{\pi}{\omega}\approx0,1s\)

\(P(x)\) là đa thức bậc 4 nên \(P(x)\) có dạng:

\(P\left(x\right)=ax^4+bx^3+cx^2+dx+e\)

\(P'\left(x\right)=4ax^3+3bx^2+2cx+d\)

\(\left\{{}\begin{matrix}P\left(1\right)=3\\P\left(3\right)=11\\P\left(5\right)=27\end{matrix}\right.\Rightarrow P\left(x\right)\) lần lượt nhận \(\left[{}\begin{matrix}x=1\\x=3\\x=5\end{matrix}\right.\) là các nghiệm của đa thức.

Ta có hệ: \(\left\{{}\begin{matrix}a+b+c+d+e=3\\81a+27b+9c+3d+e=11\\625a+125b+25c+5d+e=27\\4a+3b+2c+d=0\Rightarrow d=-4a-3b-2c\end{matrix}\right.\)

Thay vào ta được: \(\Rightarrow\left\{{}\begin{matrix}-3a-2b-c+e=3\\69a+18b+3c+e=11\\605a+110b+15c+e=27\\108a+27b+6c+\left(-4a-3b-2c\right)=0\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{7}{8}\\b=-9\\c=\dfrac{125}{4}\\e=\dfrac{151}{8}\end{matrix}\right.\) và \(d=-39\)