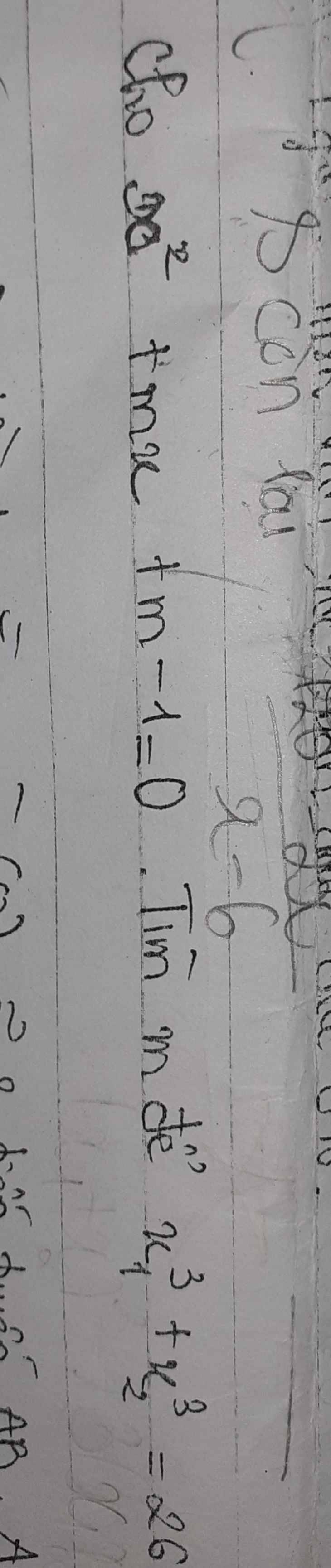 giúp e bài này với ạ
giúp e bài này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\text{Δ}=m^2-4\cdot1\cdot\left(m-1\right)\)
\(=m^2-4m+4=\left(m-2\right)^2>=0\forall m\)
=>Phương trình luôn có hai nghiệm
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-m\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)
\(x_1^3+x_2^3=26\)
=>\(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=26\)
=>\(\left(-m\right)^3-3\cdot\left(-m\right)\left(m-1\right)=26\)
=>\(-m^3+3m\left(m-1\right)=26\)
=>\(m^3-3m\left(m-1\right)=-26\)
=>\(m^3-3m^2+3m=-26\)
=>\(m^3-3m^2+3m-1=-27\)
=>\(\left(m-1\right)^3=-27\)
=>m-1=-3
=>m=-2

a: Xét ΔAIB vuông tại I và ΔAEC vuông tại E có
\(\widehat{IAB}\) chung
Do đó: ΔAIB~ΔAEC
=>\(\dfrac{AI}{AE}=\dfrac{AB}{AC}\)
=>\(AI\cdot AC=AB\cdot AE\)
b: Xét ΔCBI vuông tại I và ΔACF vuông tại F có
\(\widehat{BCI}=\widehat{CAF}\)(BC//AF)
Do đó; ΔCBI~ΔACF
=>\(\dfrac{CI}{AF}=\dfrac{CB}{AC}\)
=>\(CB\cdot AF=CI\cdot AC\)
\(AB\cdot AE+CB\cdot AF\)
\(=AI\cdot AC+CI\cdot AC\)
\(=AC\left(AI+CI\right)=AC^2\)
c: Xét tứ giác AECF có \(\widehat{AEC}+\widehat{AFC}=90^0+90^0=180^0\)
nên AECF là tứ giác nội tiếp
=>\(\widehat{FAC}=\widehat{FEC}\)
mà \(\widehat{FAC}=\widehat{BCA}\)(AD//BC)
nên \(\widehat{CEF}=\widehat{BCA}\)

Câu 1: B
Câu 2: A
Câu 3: B
Câu 4: C
Câu 5: D
Câu 6: A
Câu 7: \(\dfrac{x+2}{6}=\dfrac{-15}{2}\)
=>\(\dfrac{x+2}{6}=\dfrac{-45}{6}\)
=>x+2=-45
=>x=-47
=>Chọn C
Câu 8: B
Câu 9: C
Câu 10: A
Câu 11: \(x\cdot\dfrac{3}{4}=\dfrac{7}{8}\)
=>\(x=\dfrac{7}{8}:\dfrac{3}{4}=\dfrac{7}{8}\cdot\dfrac{4}{3}=\dfrac{28}{24}=\dfrac{7}{6}\)
=>Chọn C
Câu 12: C
Câu 13: D
Câu 14; C
Câu 15: A
Câu 16: D
II: Tự luận:
Bài 2:
a: \(3\dfrac{1}{3}x+16=13,25\)
=>\(x\cdot\dfrac{10}{3}=13,25-16=-2,75\)
=>\(x=-\dfrac{11}{4}:\dfrac{10}{3}=-\dfrac{11}{4}\cdot\dfrac{3}{10}=\dfrac{-33}{40}\)
b: \(x-43=\left(57-x\right)-50\)
=>x-43=7-x
=>2x=50
=>x=25

tk
Đáp án:4h28'
Giải thích các bước giải:
thời gian lắp 12 cái ghế, 16 cái bàn là
8.(12:3)=32(h)
đổi 7h15'=7,25h
số h lắp 12 cái ghế, 9 cái bàn là
7,25.12:9=29/3(h)
t/gian lắp 16-9=7 cái bàn là
32-29/3=20h20'
1 cái bàn hết số h là
20h20':5=4h28'

Giải:
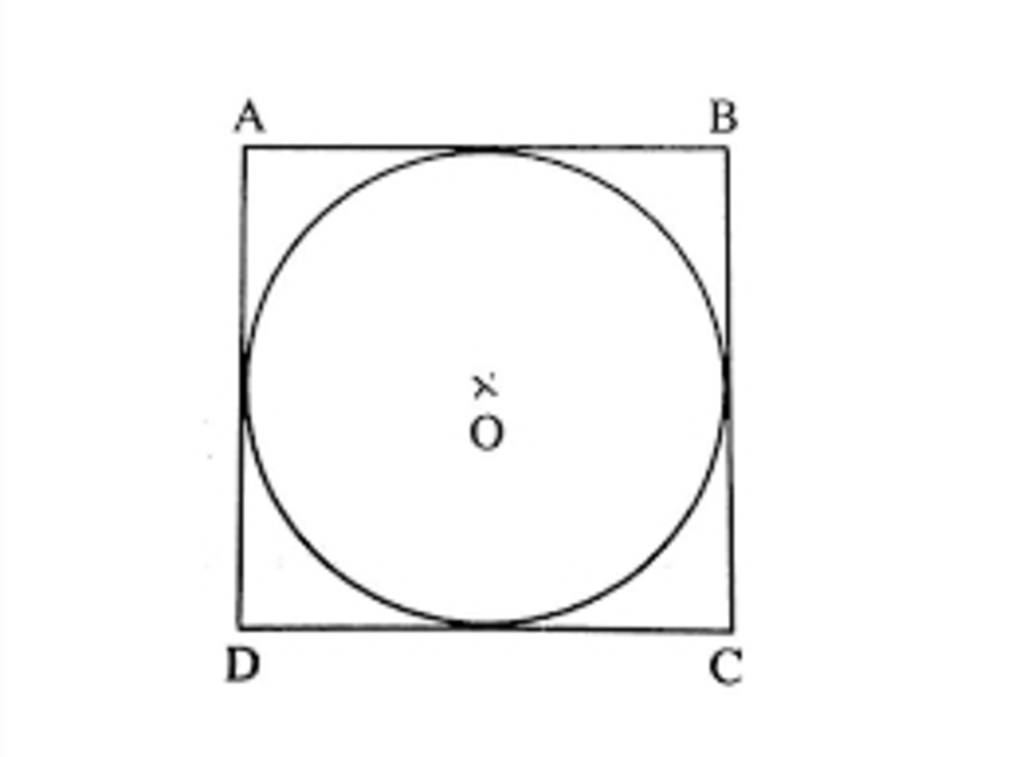
Cạnh của hình vuông chính là đường kính của hình tròn,
Diện tích hình vuông bằng: AD x AC = 28 cm2
Diện tích hình tròn bằng: AD x AC x 3,14 : 4 (cm2)
Diện tích hình tròn là: 28 x 3,14 : 4 = 21,98 (cm2)
Đáp số: 21,98 cm2

Giải:
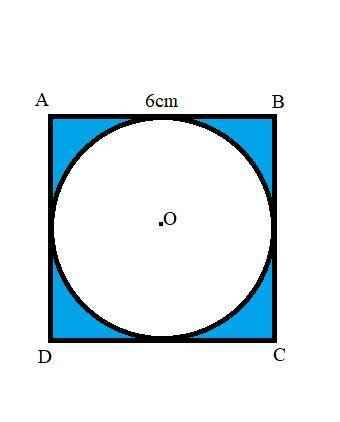
Diện tích hình vuông bằng: AB x AD = 28 cm2
Cạnh hình vuông bằng đường kính của hình tròn
Diện tích hình tròn bằng: AB x AD x 3,14 : 4
Diện tích hình tròn là: 28 x 3,14 : 4 = 21,98 (cm2)
Đáp số:...
Lời giải:
Ta thấy đường kính hình tròn chính bằng độ dài cạnh của hình vuông.
Gọi độ dài cạnh của hình vuông là $a$ (cm)
Diện tích hình vuông: $a\times a=28$ (cm2)
Bán kính hình tròn: $a:2=a\times 0,5$ (cm)
Diện tích hình tròn: $3,14\times (a\times 0,5)\times (a\times 0,5)=3,14\times 0,5\times 0,5\times a\times a=0,785\times 28 = 21,98$ (cm2)

Giải:
Số gạo còn lại sau ngày thứ nhất là:
800 x (100% - 32%) = 544 (tấn)
Số gạo ngày thứ ba xuất là:
544 x (100% - 45%) = 299,2 (tấn)
Đáp số:...
Lời giải:
Ngày thứ nhất công ty xuất được số tấn gạo là:
$800\times 32:100=256$ (tấn)
Ngày thứ hai công ty xuất được số tấn gạo là:
$(800-256)\times 45:100=244,8$ (tấn)
Ngày thứ ba công ty xuất được số tấn gạo là:
$800-256-244,8=299,2$ (tấn)
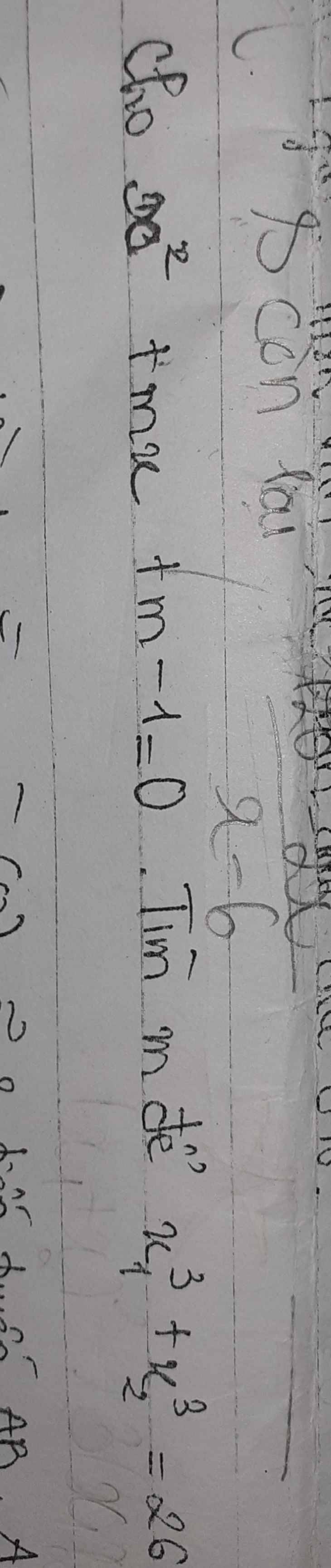


\(\Delta=m^2-4\left(m-1\right)=\left(m-2\right)^2\ge0;\forall m\in\mathbb{R}\)
\(\Rightarrow\) Phương trình đã cho có 2 nghiệm với mọi \(m\in\mathbb{R}\)
Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=m-1\end{matrix}\right.\)
Theo đề bài, ta có:
\(x_1^3+x_2^3=26\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=26\)
\(\Rightarrow\left(-m\right)^3-3\left(m-1\right)\cdot\left(-m\right)=26\)
\(\Leftrightarrow-m^3+3m-3=26\)
\(\Leftrightarrow m^3-3m+29=0\)
Nghiệm của pt này hơi xấu, bạn kiểm tra lại đề nhé.
Từ trên xuống tới dòng:
(-m)³ - 3(m - 1).(-m) = 26 em coi của bạn Toru nhé, Thầy giải tiếp chỗ đó
(-m)³ - 3(m - 1).(-m) = 26
⇔ -m³ + 3m² - 3m = 26
⇔ m³ - 3m² + 3m + 26 = 0
⇔ m³ + 2m² - 5m² - 10m + 13m + 26 = 0
⇔ (m³ + 2m²) - (5m² + 10m) + (13m + 26) = 0
⇔ m²(m + 2) - 5m(m + 2) + 13(m + 2) = 0
⇔ (m + 2)(m² - 5m + 13) = 0
⇔ m + 2 = 0 hoặc m² - 5m + 13 = 0
*) m + 2 = 0
⇔ m = -2
*) m² - 5m + 13 = 0 (2)
∆ = (-5)² - 4.1.13 = -27 < 0
⇒ Phương trình (2) vô nghiệm
Vậy m = -2