
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{a}{d}+\dfrac{c}{d}=\dfrac{a}{b}\cdot\dfrac{c}{d}\\ =>\dfrac{a}{b}\cdot\dfrac{c}{d}-\dfrac{c}{d}=\dfrac{a}{b}\\ =>\dfrac{c}{d}\cdot\left(\dfrac{a}{b}-1\right)=\dfrac{a}{b}\\ =>\dfrac{c}{d}\cdot\dfrac{a-b}{b}=\dfrac{a}{b}\\ =>\dfrac{c}{d}=\dfrac{a}{b}:\dfrac{a-b}{b}\\ =>\dfrac{c}{d}=\dfrac{a}{b}\cdot\dfrac{b}{a-b}\\ =>\dfrac{c}{d}=\dfrac{a}{a-b}\)
Vậy: ...

a) Để A là phân số thì \(n-2\ne0\Rightarrow n\ne2\)
b) \(A=-3=>\dfrac{2n-7}{n-2}=-3\)
\(=>2n-7=-3\left(n-2\right)\\ =>2n-7=-3n+6\\ =>2n+3n=6+7\\ =>5n=13\\ =>n=\dfrac{13}{5}\left(ktm\right)\)
c) \(A=\dfrac{2n-7}{n-2}=\dfrac{2n-4-3}{n-2}=\dfrac{2\left(n-2\right)-3}{n-2}=2-\dfrac{3}{n-2}\)
Để A nguyên thì: 3 ⋮ n - 2
=> n - 2 ∈ Ư(3) ={1; -1; 3; -3}
=> n ∈ {3; 1; 5; -1}
d) Để A lớn nhất thì \(\dfrac{3}{n-2}\) nhỏ nhất
=> \(\dfrac{3}{n-2}=-1\)
=> 3 = -(n - 2)
=> 3 = -n + 2
=> n = -1
e) Để A nhỏ nhất thì \(\dfrac{3}{n-2}\) lớn nhất
=> \(\dfrac{3}{n-2}=1\)
=> 3 = n - 2
=> n = 3 + 2
=> n = 5
f) Để A là phân số tối giản => ƯCLN(2n - 7; n - 2) = 1
=> ƯCLN(3; n - 2) = 1
=> n - 2 không chia hết cho 3
=> n - 2 ≠ 3k
=> n ≠ 3k + 2
g) Gọi d là ước nguyên tố của 2n - 7 và n - 2 ta có:
2n - 7 ⋮ d và n - 2 ⋮ d
=> 2n - 7 ⋮ d và 2(n - 2) ⋮ d
=> (2n - 4) - (2n - 7) ⋮ d
=> 3 ⋮ d
=> d ∈ {1; -1; 3; -3}
Mà d là STN => d = 3
Với d = 3 => 2n - 7 ⋮ 3 => 2(2n - 7) ⋮ 3 => 4n - 7 ⋮ 3
=> 3n + n - 7 ⋮ 3
=> n - 7 ⋮ 3
=> n - 7 = 3k
=> n = 3k + 7
bạn cho mình hỏi sao câu d và câu e lại là -1 và 1 thế ạ?

Tỉ số giữa 6 và mẫu số là:
\(\dfrac{1}{3}-\dfrac{2}{9}=\dfrac{3}{9}-\dfrac{2}{9}=\dfrac{1}{9}\)
Mẫu số là 6x9=54
Tử số là \(54:9\times2=6\times2=12\)
Vậy: phân số cần tìm là \(\dfrac{12}{54}\)
Đây là dạng toán nâng cao hai tỉ số, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải
Tỉ số của tử số lúc đầu và từ số lúc sau là: \(\dfrac{2}{9}\) : \(\dfrac{1}{3}\) = \(\dfrac{2}{3}\)
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Tử số lúc đầu là: 6 : (3 - 2) x 2 = 12
Mẫu số lúc đầu là: 12 : \(\dfrac{2}{9}\) = 54
Phân số cần tìm là: \(\dfrac{12}{54}\)

ĐKXĐ: \(x\ne\pm y\)
Phương trình ở dưới thiếu vế phải rồi bạn

\(10x^2+y^2+4z^2+6x-4y-4xz=-5\\ =>10x^2+y^2+4z^2+6x-4y-4xz+5=0\\ =>\left(9x^2+6x+1\right)+\left(x^2-4xz+4z^2\right)+\left(y^2-4y+4\right)=0\\ =>\left(3x+1\right)^2+\left(x-2z\right)^2+\left(y-2\right)^2=0\)
Mà: \(\left\{{}\begin{matrix}\left(3x+1\right)^2\ge0\forall x\\\left(x-2z\right)^2\ge0\forall x,z\\\left(y-2\right)^2\ge0\forall y\end{matrix}\right.=>\left(3x+1\right)^2+\left(x-2z\right)^2+\left(y-2\right)^2\ge0\forall x,y,z\)
\(=>\left\{{}\begin{matrix}3x+1=0\\x-2z=0\\y-2=0\end{matrix}\right.=>\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\z=-\dfrac{1}{6}\\y=2\end{matrix}\right.\)
\(10x^2+y^2+4z^2+6x-4y-4xz=-5\\ \Leftrightarrow\left(x^2-4xz+4z^2\right)+\left(9x^2+6x+1\right)+\left(y^2-4y+4\right)=0\\ \Leftrightarrow\left(x-2z\right)^2+\left(3x+1\right)^2+\left(y-2\right)^2=0\)
Ta thấy: \(\left\{{}\begin{matrix}\left(x-2z\right)^2\ge0\forall x,z\\\left(3x+1\right)^2\ge0\forall x\\\left(y-2\right)^2\ge0\forall y\end{matrix}\right.\)
\(\Rightarrow\left(x-2z\right)^2+\left(3x+1\right)^2+\left(y-2\right)^2\ge0\forall x,y,z\)
Mà: \(\left(x-2z\right)^2+\left(3x+1\right)^2+\left(y-2\right)^2=0\)
Do đó: \(\left\{{}\begin{matrix}x-2z=0\\3x+1=0\\y-2=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=2\\z=-\dfrac{1}{6}\end{matrix}\right.\)
#$\mathtt{Toru}$

c; C = \(\dfrac{28^{28}+28^{24}+...+28^4+1}{28^{30}+28^{28}+...+28^2+1}\)
A = 1 + 284 + 288 + 2812 + ...2828
284A = 284 + 288 + 2812 + ... + 2828 + 2832
284A - A = 284+ 288+...+2828+ 2832- (1 + 284 + 288+...+2828)
(284 - 1)A = 284 + 288+ ...+ 2828 + 2832 - 1 - 284- ...- 2828
(284 - 1)A = (2832 - 1) + (284 - 284) + (288 - 288) + ... + (2828 - 2828)
(284 - 1)A = 2832 - 1 + 0 + 0... + 0
A = (2832 - 1): (284 - 1)
Đặt B = 2830 + 2828 + ... + 282 + 1
282B = 2832 + 2830 + ... + 284 + 282
282B - B = 2832 + 2830 + ... + 284 + 282 - (2830 + 2828 +...+1)
(282 - 1)B = 2832 + 2830+...+284 + 282 - 2830 - 2828 - ... 282- 1
(282 - 1)B = (2832 - 1) + (2830 - 2830) +...+(282 - 282)
(282 - 1)B = (2832 - 1) + 0 + 0 +...+ 0
(282 - 1)B = 2832 - 1
B = (2832 - 1): (282 - 1)
C = \(\dfrac{A}{B}\) = \(\dfrac{28^{32}-1}{28^4-1}\) : \(\dfrac{28^{32}-1}{28^2-1}\)
C = \(\dfrac{28^{32}-1}{28^4-1}\) \(\times\) \(\dfrac{28^2-1}{28^{32}-1}\)
C = \(\dfrac{28^2-1}{28^4-1}\)
C = \(\dfrac{1}{785}\)
Câu d:
\(\dfrac{x-1}{99}\) + \(\dfrac{x-2}{98}\) + \(\dfrac{x-3}{97}\) = \(\dfrac{x-4}{96}\) + \(\dfrac{x-5}{95}\) + \(\dfrac{x-6}{94}\)
(\(\dfrac{x-1}{99}\)-1)+(\(\dfrac{x-2}{98}\)-1)+(\(\dfrac{x-3}{97}\)-1) = (\(\dfrac{x-4}{96}\)-1) + (\(\dfrac{x-5}{95}\)-1)+(\(\dfrac{x-6}{94}\)-1)
\(\dfrac{x-100}{99}\)+\(\dfrac{x-100}{98}\)+\(\dfrac{x-100}{97}\) = \(\dfrac{x-100}{96}\)+\(\dfrac{x-100}{95}\)+\(\dfrac{x-100}{94}\)
\(\dfrac{x-100}{99}\)+\(\dfrac{x-100}{98}\)+\(\dfrac{x-100}{97}\)- \(\dfrac{x-100}{96}\)-\(\dfrac{x-100}{95}\)-\(\dfrac{x-100}{94}\) = 0
(\(x-100\)).(\(\dfrac{1}{99}\)+\(\dfrac{1}{98}\)+\(\dfrac{1}{97}\) - \(\dfrac{1}{96}\)-\(\dfrac{1}{95}\)-\(\dfrac{1}{94}\)) = 0
Vì\(\dfrac{1}{98}< \dfrac{1}{98}< \dfrac{1}{97}< \dfrac{1}{96}< \dfrac{1}{95}< \dfrac{1}{94}\)
Nên (\(\dfrac{1}{99}\) + \(\dfrac{1}{98}\) + \(\dfrac{1}{97}\) )- (\(\dfrac{1}{96}\) + \(\dfrac{1}{95}\) +\(\dfrac{1}{94}\) )< 0
⇒\(x-100\) = 0
Vậy \(x\) = 100

Gọi số học sinh đi tham quan là \(a\)
Điều kiện: \(a\inℕ^∗;700\le a\le1200\)
Ta có:
+) Nếu xếp 30 em hay 45 em vào 1 xe thì đều thiếu 5 em
⇒\(a\) chia \(30\) hay \(45\) thiếu \(5\)
\(\Rightarrow a+5⋮30;45\)
\(\Rightarrow a+5\in BC\left(30;45\right)=\left\{0,90,180,270,360,450,540,630,720,810,900,990,1080,1170,1260,...\right\}\)
Mà \(700\le a\le1200\) nên \(705\le a+5\le1205\) suy ra:
\(a\in\left\{720,810,900,990,1080,1170\right\}\)
+) Nếu xếp 43 em vào một xe thì vừa đủ
\(\Rightarrow a⋮43\)
Do đó: \(a=1075\) (thỏa mãn điều kiện)
Vậy...
Gọi tổng số h/s là A
A:30 thiếu 5 , chia 45 cũng thiếu 5 ≠Ta có :
A+5 ∈ BCNN(45,30)700≤A≤1200
30=2.3.5
45=2.3.3.5=2.32.5
BCNN(30,45)=2.95=90
BC(30,45)={0,90,180,270,360,450,540,630,720,810,900,990,1080,1170} mà 700≤A≤1200 nên loại các số 0,90,180,270,360,450,540,630.
Nếu A là 1 trong các số trên thì phải trừ đi 5 , A ∈={715,805,895,985,1075,1165}
Vì A⋮43 nên A sẽ bằng 1075 , vậy chuyến đi đó có 1075 h/s lớp 6
Đáp số 1075 h/s

Gọi số đó có dạng \(\overline{ab}\)
Khi thêm số 0 vào giữa thì ta có số mới là: \(\overline{a0b}=100a+b\)
Mà số mới gấp 7 lần số cũ nên ta có:
\(\overline{a0b}=7\overline{ab}\\ 100a+b=7\left(10a+b\right)\\ 100a+b=70a+7b\\ 100a-70a=7b-b\\ a\left(100-70\right)=b\left(7-1\right)\\ 30a=6b\\ \dfrac{a}{b}=\dfrac{6}{30}=\dfrac{1}{5}\)
`=> a=1;b=5`
Vậy sso cần tìm là 15

`n^2+n+4` chia hết cho n + 1
`=>(n^2+n) +4` chia hết cho n + 1
`=> n(n+1)+4` chia hết cho n + 1
Mà: `n(n+1)` chia hết cho n + 1
=> 4 chia hết cho n + 1
=> n + 1 ∈ Ư(4) = {1; -1; 2; -2; 4; -4}
=> n ∈ {0; -2; 1; -3; 3; -5}
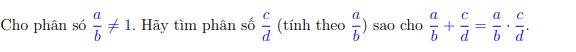
 Help!
Help!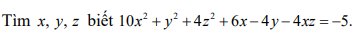
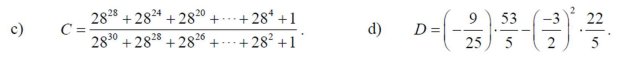
 Giúp mình với các bạn,mình cần gấp câu c1 và câu d2 ạ !
Giúp mình với các bạn,mình cần gấp câu c1 và câu d2 ạ !
Gọi mẫu số của phân số cần tìm là x
Theo đề, ta có: \(-\dfrac{11}{13}< \dfrac{9}{x}< \dfrac{-11}{15}\)
=>\(\dfrac{11}{13}>\dfrac{-9}{x}>\dfrac{11}{15}\)
=>\(\dfrac{99}{117}>\dfrac{-99}{11x}>\dfrac{99}{135}\)
=>\(\dfrac{99}{117}>\dfrac{99}{-11x}>\dfrac{99}{135}\)
=>\(-11x\in\left\{118;119;...;134\right\}\)
=>\(x\in\left\{-\dfrac{118}{11};-\dfrac{119}{11};...;\dfrac{134}{-11}\right\}\)
mà x nguyên
nên \(x\in\left\{-11;-12\right\}\)
Vậy: Hai phân số cần tìm là \(\dfrac{9}{-11};\dfrac{9}{-12}\)
=>