\(1+\dfrac{7}{n\left(n+8\right)}=\dfrac{n^2+8n+7}{n\left(n+8\right)}=\dfrac{\left(n+1\right)\left(n+7\right)}{n\left(n+8\right)}\)

\(\Rightarrow P=\left(1+\dfrac{7}{1.\left(1+8\right)}\right)\left(1+\dfrac{7}{2.\left(2+8\right)}\right)\left(1+\dfrac{7}{3.\left(3+8\right)}\right)...\left(1+\dfrac{7}{50.\left(50+8\right)}\right)\)

\(=\left(\dfrac{2.8}{1.9}\right).\left(\dfrac{3.9}{2.10}\right).\left(\dfrac{4.10}{3.11}\right)...\left(\dfrac{51.57}{50.58}\right)\)

\(=\dfrac{2.3.4...51}{1.2.3...50}.\dfrac{8.9.10...57}{9.10.11...58}=\dfrac{51}{1}.\dfrac{8}{58}=\dfrac{204}{29}\)

tui cũng ko biết đâu

@phùng thị ngọc khánh, bạn không biết thì đừng bình luận linh tinh nhé.

khó thế

có

\(\dfrac{x-y}{2x+y}=\dfrac{1}{3}\) \(\Rightarrow3\left(x-y\right)=2x+y\)

\(\Rightarrow3x-3y=2x+y\)

\(\Rightarrow x=4y\)

\(\Rightarrow T=\dfrac{x^2}{x^2+y^2}=\dfrac{\left(4y\right)^2}{\left(4y\right)^2+y^2}=\dfrac{16y^2}{16y^2+y^2}=\dfrac{16y^2}{17y^2}=\dfrac{16}{17}\)

theo đề bài ta có: x/y=4/7 => x= \(\dfrac{4}{7}y\)

Thay vào biểu thức x.y=112

=>\(\dfrac{4}{7}y^2\)=112

<=>\(y^2\)=112:\(\dfrac{4}{7}\)

<=>\(y^2\)=196

<=>\(\left[{}\begin{matrix}y=14\\y=-14\end{matrix}\right.\)

Với y=14 => x=\(\dfrac{4}{7}.14\)=\(8\)

VỚi y=-14 => x=\(\dfrac{4}{7}.\left(-14\right)\)=-8

10h30 r ngủ đi

Đây là toán nâng cao chuyên đề về tỉ lệ thức và tỉ số vận tốc. cấu trúc thi hsg. Hôm nay olm sẽ hướng dẫn em giải dạng này như sau:

Gọi vận tốc của Hoa là \(x\) (km/h); đk \(x\) > 0

Vận tốc của Mai là y (km/h); y > 0

Đổi 30 phút = 0,5 giờ; \(\dfrac{2}{5}\)giờ = 0,4 giờ 

Vì cùng một quãng đường vận tốc tỉ lệ nghịch với thời gian nên ta có:

     \(\dfrac{x}{y}\) =  \(\dfrac{0,5}{0,4}\) = \(\dfrac{5}{4}\)  ⇒ \(\dfrac{x}{5}\) = \(\dfrac{y}{4}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

    \(\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{x-y}{5-4}\) = \(\dfrac{3}{1}\) = 3 

\(x\) = 3.5 = 15; y = 3.4 = 12

Kết luận: Vận tốc của Hoa là 15 km/h; Vận tốc của Hoa là 12 km/h

Chọn ý C: 600 học sinh nhé

Chọn C.

a/

Xét tg vuông ABD và tg vuông EBD có

BD chung; \(\widehat{ABD}=\widehat{CBD}\left(gt\right)\)

=> tg ABD = tg EBD (hai tg vuông có cạnh huyền và 1 góc nhọn bằng nhau) => AB=BE

b/

Xét tg ABE có

AB=BE (cmt) => tg ABE cân tại B

Mà BD là phân giác của \(\widehat{B}\) (gt) => BD là đường cao của tg ABE (Trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao) \(\Rightarrow AE\perp BD\)

c/

Xét tg vuông ABC và tg vuông EBH có

AB=BE (cmt)

\(\widehat{ACB}=\widehat{EHB}\) (cùng phụ với \(\widehat{B}\) )

=> tg ABC = tg EHB (Hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau) => BH=BC

d/

C/m tương tự câu (b) khi xét tg BCH

\(\Rightarrow HC\perp BD\)

Mà \(AE\perp BD\left(cmt\right)\)

=> AE//HC (cùng vuông góc với BD)

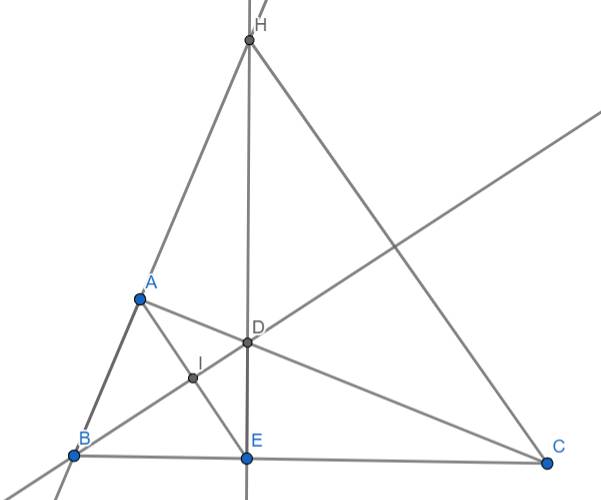
a) Xét hai tam giác vuông ABD (vuông tại A) và tam giác BDE (vuông tại E) ta có: 

BD là cạnh chung 

\(\widehat{ABD}=\widehat{DBE}\) (BD là phân giác của góc B) 

\(\Rightarrow\Delta ABD=\Delta DBE\) (cạnh huyền góc nhọn) 

\(\Rightarrow AB=BE\) (hai cạnh tương ứng) 

b) Ta có: \(\Delta ABD=\Delta DBE\left(cmt\right)\)

\(\Rightarrow\left\{{}\begin{matrix}\widehat{ADI}=\widehat{IDE}\\AD=DE\end{matrix}\right.\) 

Xét hai tam giác ADI và tam giác EDI có:

\(\widehat{ADI}=\widehat{IDE}\left(cmt\right)\) 

\(AD=DE\left(cmt\right)\)

\(ID\) là cạnh chung 

\(\Rightarrow\Delta ADI=\Delta EDI\) (c.g.c) 

\(\Rightarrow\widehat{AID}=\widehat{DIE}\) (2 cạnh t.ứng) 

Mà: \(\widehat{ADI}+\widehat{DIE}=180^o\) (kề bù) 

\(\Rightarrow\widehat{ADI}=\widehat{DIE}=\dfrac{180^o}{2}=90^o\)

Hay AE ⊥ BD 

c) Xét 2 tam giác vuông HBE (vuông tại E) và tam giác CBA (vuông tại A) ta có:

\(\widehat{HBC}\) chung 

\(AB=BE\left(cmt\right)\) 

\(\Rightarrow\Delta HBE=\Delta CBA\left(g.c.g\right)\) 

\(\Rightarrow BH=BC\) (2 cạnh t.ứng) 

d) Tam giác HBC có HB = HC (cmt) 

\(\Rightarrow\Delta HBC\) cân tại H 

Gọi F là giao điểm của BD và HC ta có: 

BF là tia phân của góc B 

Nên đồng thời BF cũng là đường cao của tam giác HBC 

\(\Rightarrow BF\perp HC\) (1)

Mà: \(BD\perp AE\) hay \(BF\perp AE\left(cmt\right)\) (2)

Từ (1) và (2) ta có: 

AE//HC (đpcm)