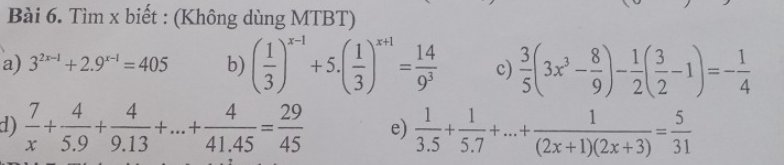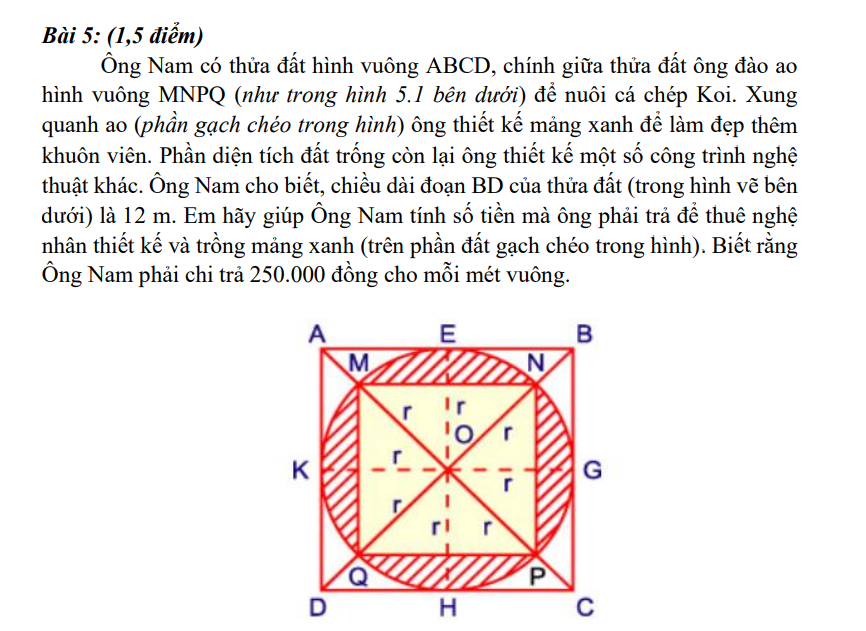
Giải:

Diện tích của hình vuông ABCD là: 12 x 12 : 2 = 72 (m²)

Diện tích của hình tròn tâm O bán kính OK là:

  KG.EH.3,14 : 4 = \(\dfrac{1}{4}\)KG.EH = \(\dfrac{3,14}{4}\)S_ABCD = 72 x \(\dfrac{3,14}{4}\) = 56,52 (m²)

     ⇒ MP.QN.3,14:4 = 56,52

    ⇒ MP.QN = 56,52 x 4 : 3,14 = 72

 Diện tích hình vuông MNPQ là:

   MP.QN : 2 = 72: 2 = 36 (m²)

Diện tích phần gạch chéo là: 

     56,52  - 36  = 20,52 (m²)

    Số tiền ông Nam phải chi trả cho nghệ nhân trang trí phần diện tích gạch chéo là:

            250 000 x 20,52  = 5 130 000 (đồng)

Kết luận:...

\(\overline{abc4}-\overline{abc}-1111\\ \overline{abc}\cdot10+4-\overline{abc}=1111\\ \overline{abc}\cdot\left(10-1\right)=1111-4\\ \overline{abc}\cdot9=1107\\ \overline{abc}=1107:9\\ \overline{abc}=123\) 

_____________________

\(\overline{ab5}=\overline{ab}+230\\ \overline{ab}\cdot10+5=\overline{ab}+230\\ \overline{ab}\cdot10-\overline{ab}=230-5\\ =>\overline{ab}\cdot\left(10-1\right)=225\\ =>\overline{ab}\cdot9=225\\ =>\overline{ab}=225:9\\ =>\overline{ab}=25\)

\(\left(x+\dfrac{4}{3}\right)^4=\dfrac{1}{81}\\ =>\left(x+\dfrac{4}{3}\right)^4=\left(\dfrac{1}{3}\right)^4\)

TH1: `x+4/3=1/3`

`=>x=1/3-4/3`

`=>x=-3/3`

`=>x=-1`

TH2: `x+4/3=-1/3`

`=>x=-1/3-4/3`

`=>x=-5/3`

Vậy: ...

\(\left(x-\dfrac{2}{7}\right)^5=32\\ =>\left(x-\dfrac{2}{7}\right)^5=2^5\\ =>x-\dfrac{2}{7}=2\\ =>x=\dfrac{2}{7}+2\\ =>x=\dfrac{16}{7}\)

`#3107.101107`

- Các số trong tập hợp cách nhau `5` đơn vị

Số phần tử của tập hợp X:

\(\left(277-2\right)\div5+1=56\) (phần tử)

Vậy, số phần tử của tập hợp X là `56.`

\(a)3^{2x-1}+2\cdot9^{x-1}=405\\ =>3^{2x-1}+2\cdot\left(3^2\right)^{x-1}=405\\ =>3^{2x-1}+2\cdot3^{2x-2}=405\\ =>3^{2x-2}\cdot\left(3+2\right)=405\\ =>3^{2x-2}\cdot5=405\\ =>3^{2x-2}=\dfrac{405}{5}=81\\ =>3^{2x-2}=3^4\\ =>2x-2=4\\ =>2x=4+2=6\\ =>x=\dfrac{6}{2}\\ =>x=3\)

\(b)\left(\dfrac{1}{3}\right)^{x-1}+5\left(\dfrac{1}{3}\right)^{x+1}=\dfrac{14}{9^3}\\ =>\left(\dfrac{1}{3}\right)^{x-1}\left(1+5\cdot\dfrac{1}{3^2}\right)=\dfrac{14}{729}\\ =>\left(\dfrac{1}{3}\right)^{x-1}\cdot\dfrac{14}{9}=\dfrac{14}{729}\\ =>\left(\dfrac{1}{3}\right)^{x-1}=\dfrac{14}{729}:\dfrac{14}{9}\\ =>\left(\dfrac{1}{3}\right)^{x-1}=\dfrac{9}{729}=\dfrac{1}{81}\\ =>\left(\dfrac{1}{3}\right)^{x-1}=\left(\dfrac{1}{3}\right)^4\\ =>x-1=4\\ =>x=1+4\\ =>x=5\)

\(c)\dfrac{3}{5}\left(3x^3-\dfrac{8}{9}\right)-\dfrac{1}{2}\left(\dfrac{3}{2}-1\right)=-\dfrac{1}{4}\\ =>\dfrac{3}{5}\left(3x^3-\dfrac{8}{9}\right)-\dfrac{1}{2}\cdot\dfrac{1}{2}=-\dfrac{1}{4}\\ =>\dfrac{3}{5}\left(3x^3-\dfrac{8}{9}\right)-\dfrac{1}{4}=-\dfrac{1}{4}\\ =>\dfrac{3}{5}\left(3x^3-\dfrac{8}{9}\right)=0\\ =>3x^3-\dfrac{8}{9}=0\\ =>3x^3=\dfrac{8}{9}\\ =>x^3=\dfrac{8}{9}:3=\dfrac{8}{27}\\ =>x^3=\left(\dfrac{2}{3}\right)^3\\ =>x=\dfrac{2}{3}\)

a: \(3^{2x-1}+2\cdot9^{x-1}=405\)

=>\(\dfrac{3^{2x}}{3}+2\cdot3^{2x-2}=405\)

=>\(\dfrac{1}{3}\cdot3^{2x}+2\cdot3^{2x}\cdot\dfrac{1}{9}=405\)

=>\(3^{2x}\cdot\left(\dfrac{1}{3}+\dfrac{2}{9}\right)=405\)

=>\(3^{2x}\cdot\dfrac{5}{9}=405\)

=>\(3^{2x}=405:\dfrac{5}{9}=405\cdot\dfrac{9}{5}=81\cdot9=3^6\)

=>2x=6

=>x=3

b: \(\left(\dfrac{1}{3}\right)^{x-1}+5\cdot\left(\dfrac{1}{3}\right)^{x+1}=\dfrac{14}{9^3}\)

=>\(\left(\dfrac{1}{3}\right)^x\cdot3+5\cdot\left(\dfrac{1}{3}\right)^x\cdot\dfrac{1}{3}=\dfrac{14}{9^3}\)

=>\(\left(\dfrac{1}{3}\right)^x\cdot\left(3+\dfrac{5}{3}\right)=\dfrac{14}{9^3}\)

=>\(\left(\dfrac{1}{3}\right)^x=\dfrac{14}{3^6}:\dfrac{14}{3}=\dfrac{3}{3^6}=\dfrac{1}{3^5}\)

=>x=5

c: \(\dfrac{3}{5}\left(3x^3-\dfrac{8}{9}\right)-\dfrac{1}{2}\left(\dfrac{3}{2}-1\right)=-\dfrac{1}{4}\)

=>\(\dfrac{9}{5}x^3-\dfrac{24}{45}-\dfrac{1}{2}\cdot\dfrac{1}{2}+\dfrac{1}{4}=0\)

=>\(\dfrac{9}{5}x^3=\dfrac{24}{45}=\dfrac{8}{15}\)

=>\(x^3=\dfrac{8}{15}:\dfrac{9}{5}=\dfrac{8}{15}\cdot\dfrac{5}{9}=\dfrac{40}{135}=\dfrac{8}{27}=\left(\dfrac{2}{3}\right)^3\)

=>\(x=\dfrac{2}{3}\)

d: \(\dfrac{7}{x}+\dfrac{4}{5\cdot9}+\dfrac{4}{9\cdot13}+...+\dfrac{4}{41\cdot45}=\dfrac{29}{45}\)

=>\(\dfrac{7}{x}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{13}+...+\dfrac{1}{41}-\dfrac{1}{45}=\dfrac{29}{45}\)

=>\(\dfrac{7}{x}+\dfrac{9}{45}-\dfrac{1}{45}=\dfrac{29}{45}\)

=>\(\dfrac{7}{x}=\dfrac{29}{45}-\dfrac{8}{45}=\dfrac{21}{45}=\dfrac{7}{15}\)

=>x=15

e: \(\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{\left(2x+1\right)\left(2x+3\right)}=\dfrac{5}{31}\)

=>\(\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{\left(2x+1\right)\left(2x+3\right)}=\dfrac{10}{31}\)

=>\(\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{2x+1}-\dfrac{1}{2x+3}=\dfrac{10}{31}\)

=>\(\dfrac{1}{3}-\dfrac{1}{2x+3}=\dfrac{10}{31}\)

=>\(\dfrac{1}{2x+3}=\dfrac{1}{3}-\dfrac{10}{31}=\dfrac{1}{93}\)

=>2x+3=93

=>2x=90

=>x=45

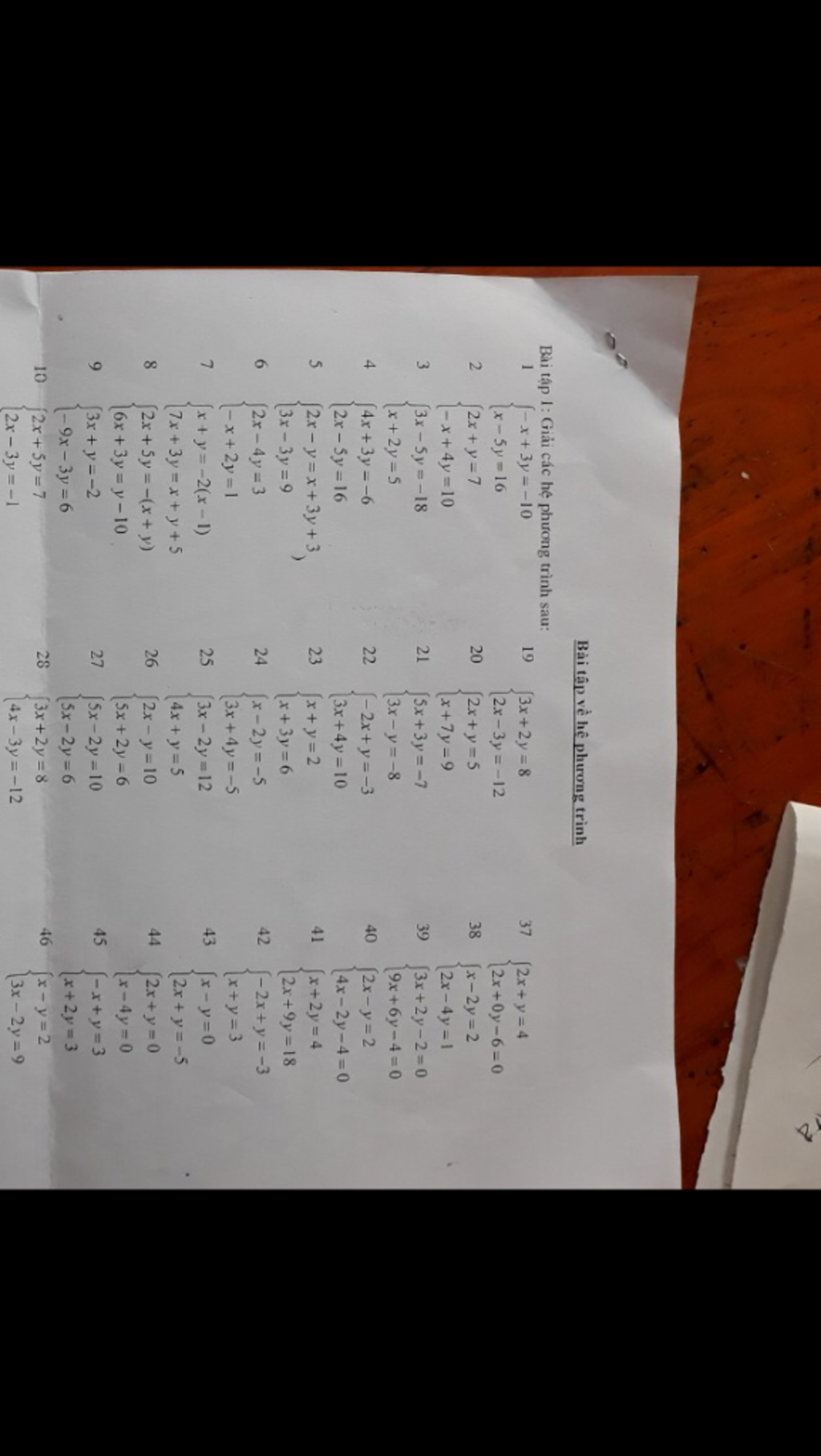
\(1.\left\{{}\begin{matrix}-x+3y=-10\\x-5y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2y=6\\x-5y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{6}{-2}=-3\\x-5\cdot\left(-3\right)=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\x+15=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=16-15=1\end{matrix}\right.\\ 2.\left\{{}\begin{matrix}2x+y=7\\-x+4y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=7\\-2x+8y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=7\\9x=27\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+y=7\\x=\dfrac{27}{9}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\cdot3+y=7\\x=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=7-6=1\\x=3\end{matrix}\right.\) 

\(3.\left\{{}\begin{matrix}3x-5y=-18\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-5y=-18\\3x+6y=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x+2\cdot\left(-3\right)=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=5+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=11\end{matrix}\right.\\ 4.\left\{{}\begin{matrix}4x+3y=-6\\2x-5y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=-6\\4x-10y=32\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13y=-38\\2x-5y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\2x-5\cdot\dfrac{-38}{13}=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\2x+\dfrac{190}{13}=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\2x=16-\dfrac{190}{13}=\dfrac{18}{13}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\x=\dfrac{18}{13}:2=\dfrac{9}{13}\end{matrix}\right.\)

20: \(\left\{{}\begin{matrix}2x+y=5\\x+7y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=5\\2x+14y=18\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x+14y-2x-y=18-5\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13y=13\\2x=5-y\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=1\\2x=5-1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)

21: \(\left\{{}\begin{matrix}5x+3y=-7\\3x-y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+3y=-7\\9x-3y=-24\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}5x+3y+9x-3y=-7-24\\3x-y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}14x=-31\\y=3x+8\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-\dfrac{31}{14}\\y=3\cdot\dfrac{-31}{14}+8=-\dfrac{93}{14}+\dfrac{112}{14}=\dfrac{19}{14}\end{matrix}\right.\)

22: \(\left\{{}\begin{matrix}-2x+y=-3\\3x+4y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3+2x\\3x+4\left(2x-3\right)=10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=2x-3\\3x+8x-12=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=22\\y=2x-3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=2\\y=2\cdot2-3=4-3=1\end{matrix}\right.\)

23: \(\left\{{}\begin{matrix}x+y=2\\x+3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+3y-x-y=6-2\\x+y=2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2y=4\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=2-y=2-2=0\end{matrix}\right.\)

24: \(\left\{{}\begin{matrix}x-2y=-5\\3x+4y=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-4y=-10\\3x+4y=-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-4y+3x+4y=-10-5\\x-2y=-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}5x=-15\\2y=x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\2y=-3+5=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=1\end{matrix}\right.\)

25: \(\left\{{}\begin{matrix}3x-2y=12\\4x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=12\\8x+2y=10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x-2y+8x+2y=12+10\\4x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=22\\y=5-4x\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=2\\y=5-4\cdot2=5-8=-3\end{matrix}\right.\)

26: \(\left\{{}\begin{matrix}2x-y=10\\5x+2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-2y=20\\5x+2y=6\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}4x-2y+5x+2y=20+6\\2x-y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=26\\y=2x-10\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{26}{9}\\y=2x-10=2\cdot\dfrac{26}{9}-10=\dfrac{52}{9}-10=-\dfrac{38}{9}\end{matrix}\right.\)

27: \(\left\{{}\begin{matrix}5x-2y=10\\5x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-2y-5x+2y=10-6\\5x-2y=6\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}0x=4\\2y=5x-6\end{matrix}\right.\Leftrightarrow\left(x;y\right)\in\varnothing\)

28: \(\left\{{}\begin{matrix}3x+2y=8\\4x-3y=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12x+8y=32\\12x-9y=-36\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}12x+8y-12x+9y=32+36\\3x+2y=8\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}17y=68\\3x=8-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\3x=8-2\cdot4=8-8=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=0\\y=4\end{matrix}\right.\)

37: \(\left\{{}\begin{matrix}2x+y=4\\2x+0y-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=6\\y=4-2x=4-6=-2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)

38: \(\left\{{}\begin{matrix}x-2y=2\\2x-4y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-4y=4\\2x-4y=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-4y-2x+4y=4-1\\x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0y=3\\x-2y=2\end{matrix}\right.\)

=>\(\left(x;y\right)\in\varnothing\)

39: \(\left\{{}\begin{matrix}3x+2y-2=0\\9x+6y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+2y=2\\9x+6y=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}9x+6y=6\\9x+6y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0y=2\\3x+2y=2\end{matrix}\right.\Leftrightarrow\left(x;y\right)\in\varnothing\)

40: \(\left\{{}\begin{matrix}2x-y=2\\4x-2y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y=2\\4x-2y=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x-y=2\\2x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0x=0\\y=2x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in R\\y=2x-2\end{matrix}\right.\)

41: \(\left\{{}\begin{matrix}x+2y=4\\2x+9y=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=8\\2x+9y=18\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x+9y-2x-4y=18-8\\x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=10\\x=4-2y\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=2\\x=4-2\cdot2=4-4=0\end{matrix}\right.\)

42: \(\left\{{}\begin{matrix}-2x+y=-3\\x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+y-x-y=-3-3\\x+y=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}-3x=-6\\y=3-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3-2=1\end{matrix}\right.\)

43: \(\left\{{}\begin{matrix}x-y=0\\2x+y=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y+2x+y=0-5\\x=y\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x=-5\\y=x\end{matrix}\right.\Leftrightarrow y=x=-\dfrac{5}{3}\)

44: \(\left\{{}\begin{matrix}2x+y=0\\x-4y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2x\\x-4\cdot\left(-2x\right)=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}9x=0\\y=-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0=0\end{matrix}\right.\)

45: \(\left\{{}\begin{matrix}-x+y=3\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x+y+x+2y=3+3\\x+2y=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3y=6\\x=3-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=3-2\cdot2=3-4=-1\end{matrix}\right.\)

46: \(\left\{{}\begin{matrix}x-y=2\\3x-2y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-3y=6\\3x-2y=9\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x-3y-2x+2y=6-9\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-y=-3\\x=y+2\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=3\\x=3+2=5\end{matrix}\right.\)

\(a)\left(\dfrac{2}{3}\right)^5=\dfrac{2^5}{3^5}=\dfrac{32}{243}\\ \left(\dfrac{-2}{3}\right)^5=\dfrac{\left(-2\right)^5}{3^5}=\dfrac{-32}{243}\\ \left(-1\dfrac{3}{4}\right)^2=\left(-\dfrac{7}{4}\right)^2=\dfrac{\left(-7\right)^2}{4^2}=\dfrac{49}{16}\\ \left(-0,1\right)^4=\left(-\dfrac{1}{10}\right)^4=\dfrac{\left(-1\right)^4}{10^4}=\dfrac{1}{10000}\)

\(b)\dfrac{90^3}{15^3}=\left(\dfrac{90}{15}\right)^3=6^3=216\\ \dfrac{790^4}{79^4}=\left(\dfrac{790}{79}\right)^4=10^4=10000\\ \dfrac{3^2}{15^2}=\left(\dfrac{3}{15}\right)^2=\left(\dfrac{1}{5}\right)^2=\dfrac{1^2}{5^2}=\dfrac{1}{25}\\ \dfrac{\left(-\dfrac{1}{2}\right)^n}{\left(-\dfrac{1}{2}\right)^{n-1}}=\left(-\dfrac{1}{2}\right)^{n-\left(n-1\right)}=\left(-\dfrac{1}{2}\right)^{n-n+1}=\left(-\dfrac{1}{2}\right)\)