Cho mình xin vài đề về khóa lưỡng phân với ạa!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Những tia trên hình vẽ là Ex,Ey,Em,En,Ct,CK,Cn
Đoạn thẳng: EK,EC,CK
b: Các cặp tia đối nhau là:
Ex;Ey
Kx;Ky
Cn;CE
CK,Ct

\(A=\dfrac{1}{2}+\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+...+\left(\dfrac{3}{2}\right)^{2023}\)
Đặt: \(C=\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+...+\left(\dfrac{3}{2}\right)^{2023}\)
\(\dfrac{3}{2}C=\left(\dfrac{3}{2}\right)^2+\left(\dfrac{3}{2}\right)^3+...+\left(\dfrac{3}{2}\right)^{2024}\)
\(\dfrac{3}{2}C-C=\left(\dfrac{3}{2}\right)^2+\left(\dfrac{3}{2}\right)^3+...+\left(\dfrac{3}{2}\right)^{2024}-\dfrac{3}{2}-\left(\dfrac{3}{2}\right)^2-...-\left(\dfrac{3}{2}\right)^{2023}\)
\(\dfrac{1}{2}C=\left(\dfrac{3}{2}\right)^{2024}-\dfrac{3}{2}\)
\(C=2\left(\dfrac{3}{2}\right)^{2024}-3\)
\(\Rightarrow A=\dfrac{1}{2}+2\left(\dfrac{3}{2}\right)^{2024}-3\)
\(=2\left(\dfrac{3}{2}\right)^{2024}-\dfrac{5}{2}\)
\(\Rightarrow A-B=2\left(\dfrac{3}{2}\right)^{2024}-\dfrac{5}{2}-2\left(\dfrac{3}{2}\right)^{2024}=-\dfrac{5}{2}\)

Xác suất thực nghiệm không phải mặt 4 chấm là:
\(\dfrac{40-13}{40}=\dfrac{27}{40}\)

Đa dạng sinh học được hiểu là sự phong phú, đa dạng về nguồn gen, giống, loài sinh vật và hệ sinh thái trong tự nhiên.
Đa dạng sinh học được chia theo 3 mức độ:
– Ở cấp quần thể đa dạng sinh học bao gồm sự khác biệt về gen giữa các loài, khác biệt về gen giữa các quần thể sống cách ly nhau về địa lý cũng như khác biệt giữa các cá thể cùng chung sống trong một quần thể.
– Đa dạng sinh học ở cấp loài bao gồm toàn bộ các sinh vật sống trên trái đất, từ vi khuẩn đến các loài thực, động vật và các loài nấm.
– Đa dạng sinh học còn bao gồm cả sự khác biệt giữa các quần xã mà trong đó các loài sinh sống và các hệ sinh thái, nơi mà các loài cũng như các quần xã sinh vật tồn tại và cả sự khác biệt của các mối tương tác giữa chúng với nhau.

a) O nằm giữa A và B nên:
\(AB=OA+OB\)
\(\Rightarrow OA=1,5+3=4,5\left(cm\right)\)
b) C nằm giữa O và B
\(OB=OC+BC\)
\(\Rightarrow BC=OB-OC\)
\(\Rightarrow BC=3-1,5=1,5\left(cm\right)\)
\(OC=BC=1,5\left(cm\right)\)


TH1: với \(a>b\)
\(\dfrac{a}{b}-1=\dfrac{a-b}{b}\)
\(\dfrac{a+n}{b+n}-1=\dfrac{a+n-\left(b+n\right)}{b+n}=\dfrac{a-b}{b+n}\)
Mà: \(b+n>b\)
\(\Rightarrow\dfrac{a-b}{b+n}< \dfrac{a-b}{b}\)
\(\Rightarrow\dfrac{a+n}{b+n}-1< \dfrac{a}{b}-1\)
\(\Rightarrow\dfrac{a+n}{b+n}< \dfrac{a}{b}\)
TH2: với \(a< b\)
\(1-\dfrac{a}{b}=\dfrac{b-a}{b}\)
\(1-\dfrac{a+n}{b+n}=\dfrac{\left(b+n\right)-\left(a+n\right)}{b+n}=\dfrac{b-a}{b+n}\)
Mà: \(b+n>b\)
\(\Rightarrow\dfrac{b-a}{b+n}< \dfrac{b-a}{b}\)
\(\Rightarrow1-\dfrac{a+n}{b+n}< 1-\dfrac{a}{b}\)
\(\Rightarrow\dfrac{a+n}{b+n}>\dfrac{a}{b}\)
TH3: \(a=b\)
\(\dfrac{a+n}{b+n}=\dfrac{a+n}{a+n}=1\)
\(\dfrac{a}{b}=\dfrac{a}{a}=1\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{a+n}{b+n}=1\)

\(S=\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+...+\dfrac{1}{512}\\ 2S=1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{256}\\ 2S-S=\left(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+...+\dfrac{1}{256}\right)-\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+...+\dfrac{1}{512}\right)\\ S=1-\dfrac{1}{512}=\dfrac{511}{512}\)
Lời giải:
$S=\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+...+\frac{1}{2^9}$
$2S=1+\frac{1}{2}+\frac{1}{2^2}+....+\frac{1}{2^8}$
$\Rightarrow 2S-S=1-\frac{1}{2^9}$
$\Rightarrow S=1-\frac{1}{2^9}$

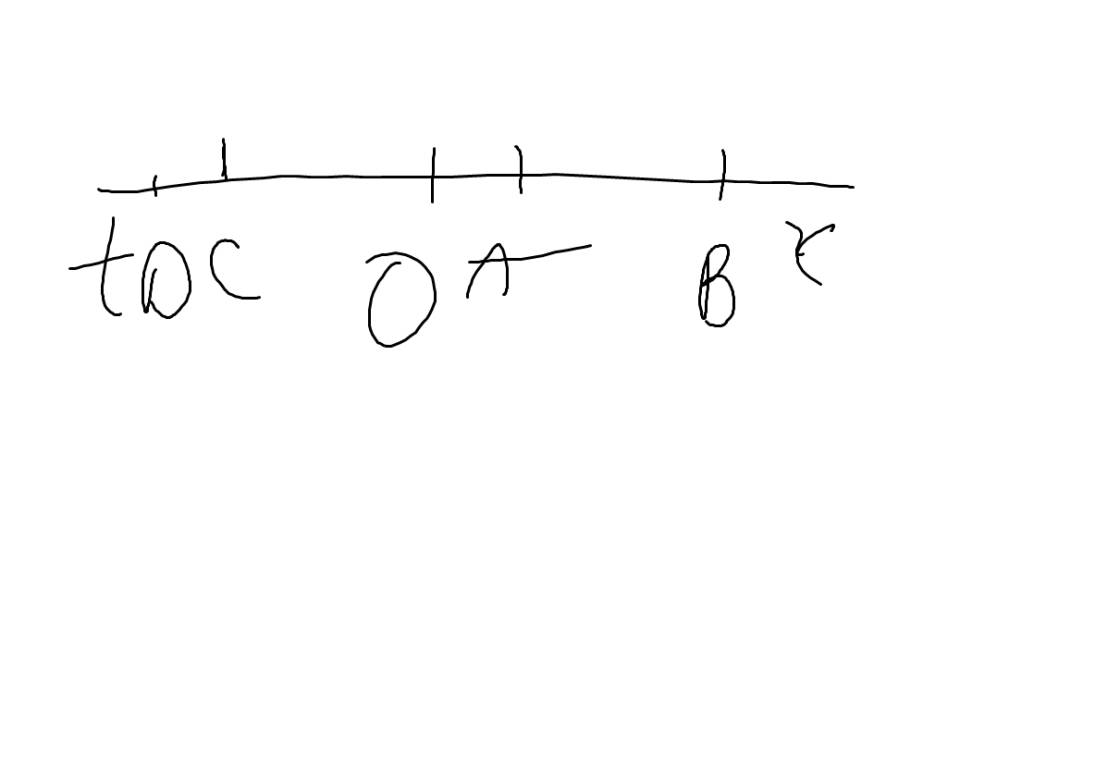
Bạn tham khảo đề trên mạng nha.
Bạn tham khảo trên mạng nhé!