
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{n-5}{n-3}=\dfrac{n-3-2}{n-3}=1-\dfrac{2}{n-3}\)
Để \(\dfrac{n-5}{n-3}\) nguyên thì \(n-3\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
Ta có bảng sau:
| \(n-3\) | \(-2\) | \(-1\) | \(1\) | \(2\) |
| \(n\) | \(1\) | \(2\) | \(4\) | \(5\) |
Vậy để \(\dfrac{n-5}{n-3}\) nguyên thì \(n\in\left\{1;2;4;5\right\}\)
Ta có: \(\dfrac{n-5}{n-3}=\dfrac{n-3-2}{n-3}=1-\dfrac{2}{n-3}\)
Để \(\dfrac{n-5}{n-3}\) nguyên
thì \(1-\dfrac{2}{n-3}\) nguyên
\(\Rightarrow2⋮n-3\)
\(\Rightarrow n-3\inƯ\left(2\right)=\left\{1;-1;2;-2\right\}\)
Lập bảng
| n-3 | 1 | -1 | 2 | -2 |
| n | 4 | 2 | 5 | 1 |
Vậy nếu \(n\in\left\{4;2;5;1\right\}\) thì \(\dfrac{n-5}{n-3}\) có giá trị nguyên

a: C là trung điểm của AB
=>\(CA=CB=\dfrac{AB}{2}=3\left(cm\right)\)
D là trung điểm của CB
=>\(DC=DB=\dfrac{CB}{2}=1,5\left(cm\right)\)
Ta có: C nằm giữa A và B
mà D nằm giữa C và B
nên C nằm giữa A và D
=>AC+CD=AD
=>AD=3+1,5=4,5(cm)
b: Gọi số điểm đã lấy thêm là x(điểm)
=>Có x+4 điểm
Theo đề, ta có: \(C^2_{x+4}=351\)
=>\(\dfrac{\left(x+4\right)!}{\left(x+2\right)!\cdot2!}=351\)
=>\(\left(x+3\right)\left(x+4\right)=351\cdot2=702\)
=>\(x^2+7x+12-702=0\)
=>\(x^2+7x-690=0\)
=>(x+30)(x-23)=0
=>\(\left[{}\begin{matrix}x=-30\left(loại\right)\\x=23\left(nhận\right)\end{matrix}\right.\)
Vậy: Đã lấy thêm 23 điểm

2.(y+1)\(\ge2\) và x2\(\ge0\)
Vậy VT\(\ge2\)
nên y = 0 và x = 0

Lời giải:
$S=\frac{1}{4}+\frac{2}{4^2}+\frac{3}{4^3}+...+\frac{2023}{4^{2023}}$
$4S=1+\frac{2}{4}+\frac{3}{4^2}+\frac{4}{4^3}+.....+\frac{2023}{4^{2022}}$
$\Rightarrow 4S-S=1+\frac{1}{4}+\frac{1}{4^2}+\frac{1}{4^3}+....+\frac{1}{4^{2022}}-\frac{2023}{4^{2023}}$
$\Rightarrow 3S+\frac{2023}{4^{2023}}=1+\frac{1}{4}+\frac{1}{4^2}+\frac{1}{4^3}+....+\frac{1}{4^{2022}}$
$\Rightarrow 4(3S+\frac{2023}{4^{2023}})=4+1+\frac{1}{4}+\frac{1}{4^2}+....+\frac{1}{4^{2021}}$
$\Rightarrow 4(3S+\frac{2023}{4^{2023}})-(3S+\frac{2023}{4^{2023}})=4-\frac{1}{4^{2022}}$
$\Rightarrow 3(3S+\frac{2023}{4^{2023}})=4-\frac{1}{4^{2022}}$
$9S=4-\frac{1}{4^{2022}}-\frac{2.2023}{4^{2023}}<4$
$\Rightarrow S< \frac{4}{9}< \frac{1}{2}$

a: \(\left(\dfrac{1}{24}-\dfrac{3}{16}\right):\left(-\dfrac{3}{8}+\dfrac{1}{2}\right)\)
\(=\dfrac{2-9}{48}:\dfrac{-3+4}{8}\)
\(=\dfrac{-7}{48}\cdot\dfrac{8}{1}=\dfrac{-7}{6}\)
b: \(\dfrac{-5}{7}:\left(5-4\dfrac{4}{7}\right)+\left(15\dfrac{1}{3}\cdot\dfrac{-1}{23}\right)\)
\(=\dfrac{-5}{7}:\left(5-\dfrac{32}{7}\right)+\dfrac{46}{3}\cdot\dfrac{-1}{23}\)
\(=\dfrac{-5}{7}:\dfrac{3}{7}+\dfrac{-2}{3}\)
\(=\dfrac{-5}{3}+\dfrac{-2}{3}=\dfrac{-7}{3}\)
c: \(\left(-1\dfrac{2}{3}\cdot1\dfrac{4}{5}+2\dfrac{5}{6}\right):\left(\dfrac{1}{6}-\dfrac{3}{4}\right)\)
\(=\left(-\dfrac{5}{3}\cdot\dfrac{9}{5}+\dfrac{17}{6}\right):\left(\dfrac{2-9}{12}\right)\)
\(=\left(-3+\dfrac{17}{6}\right):\dfrac{-7}{12}\)
\(=\dfrac{-1}{6}\cdot\dfrac{12}{-7}=\dfrac{12}{42}=\dfrac{2}{7}\)
d: \(\left(\dfrac{1}{3^2}-\dfrac{1}{7^2}\right)\cdot\left(\dfrac{1}{4^2}-\dfrac{1}{7^2}\right)\cdot...\cdot\left(\dfrac{1}{49^2}-\dfrac{1}{7^2}\right)\)
\(=\left(\dfrac{1}{7^2}-\dfrac{1}{7^2}\right)\cdot\left(\dfrac{1}{3^2}-\dfrac{1}{7^2}\right)\cdot...\left(\dfrac{1}{49^2}-\dfrac{1}{7^2}\right)\)
\(=0\left(\dfrac{1}{3^2}-\dfrac{1}{7^2}\right)\cdot...\cdot\left(\dfrac{1}{49^2}-\dfrac{1}{7^2}\right)\)
=0
e: \(\left(1-\dfrac{2}{3}\right)\left(1-\dfrac{2}{5}\right)\cdot...\cdot\left(1-\dfrac{2}{2023}\right)\)
\(=\dfrac{1}{3}\cdot\dfrac{3}{5}\cdot\dfrac{5}{7}\cdot...\cdot\dfrac{2021}{2023}=\dfrac{1}{2023}\)

Câu 7:
a: Số cần tìm là \(24:\dfrac{2}{3}=24\cdot\dfrac{3}{2}=36\)
b: Số cần tìm là \(36:\dfrac{1}{2}=72\)
c: Số cần tìm là \(-72:\dfrac{3}{4}=-72\cdot\dfrac{4}{3}=-24\cdot4=-96\)
d: Số cần tìm là \(-24:\dfrac{2}{5}=-24\cdot\dfrac{5}{2}=-60\)
Câu 6:
a: 1/5 của 25 là \(\dfrac{1}{5}\cdot25=5\)
b: 1/4 của 16 là \(\dfrac{1}{4}\cdot16=4\)
c: 2/3 của 27 là \(\dfrac{2}{3}\cdot27=18\)
d: 2/5 của 20 là \(\dfrac{2}{5}\cdot20=8\)

\(\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{9}\right)\cdot...\cdot\left(1-\dfrac{1}{900}\right)\)
\(=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\cdot...\cdot\left(1-\dfrac{1}{30}\right)\cdot\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{3}\right)\cdot...\cdot\left(1+\dfrac{1}{30}\right)\)
\(=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot...\cdot\dfrac{29}{30}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{31}{30}\)
\(=\dfrac{1}{30}\cdot\dfrac{31}{2}=\dfrac{31}{60}\)

a/
$\frac{1011}{1010}=1+\frac{1}{1010}$
$\frac{2023}{2021}=1+\frac{2}{2021}< 1+\frac{2}{2020}=1+\frac{1}{1010}$
$\Rightarrow \frac{1011}{1010}> \frac{2023}{2021}$
b/
\(2023A=\frac{2023^{2023}+2023}{2023^{2023}+1}=1+\frac{2022}{2023^{2023}+1}> 1+\frac{2022}{2023^{2024}+1}=\frac{2023^{2024}+2023}{2023^{2024}+1}=2023B\)
$\Rightarrow A> B$

|x-3|=20
=>\(\left[{}\begin{matrix}x-3=20\\x-3=-20\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=23\\x=-17\end{matrix}\right.\)

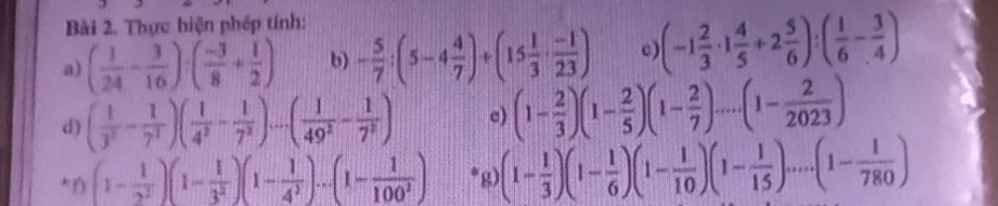
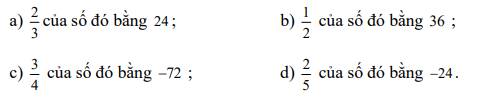
a: Các cặp tia đối nhau gốc O là:
Ox;Oy
OA và OB
Ox và OB
Oy và OA
b: vì OA và OB là hai tia đối nhau
nên O nằm giữa A và B
=>AB=OA+OB=2+3=5(cm)