\(A=1+\dfrac{3}{2}+\dfrac{7}{6}+...+\dfrac{9901}{9900}\)

\(=1+1+\dfrac{1}{2}+1+\dfrac{1}{6}+...+1+\dfrac{1}{9900}\)

\(=100+\left(\dfrac{1}{2}+\dfrac{1}{6}+...+\dfrac{1}{9900}\right)\)

\(=100+\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)

\(=100+\left(1-\dfrac{1}{100}\right)=100+\dfrac{99}{100}=\dfrac{10099}{100}\)

`A = 1 + 3/2 + 7/6 + .. + 9901/9900`

`A = 1 + 1 + 1/2 + 1 + 1/6 + .. + 1 + 1/9900`

`A = (1+1+1+...+1) + (1/(1.2) + 1/(2.3) + ... + 1/(99.100))`

Đặt `B = 1/(1.2) + 1/(2.3) + ... + 1/(99.100); C = 1+1+1+...+1`

Số số hạng trong B là: 

`(99 - 1) : 1 + 1= 99` (số hạng)

Số số hạng trong C là: 

`99 + 1 = 100` (số hạng)

(Vì có thêm số hạng 1 ở ngoài)

`B = 1 - 1/2 + 1/2 - 1/3 + ... + 1/99 - 1/100`

`= 1 - 1/100`

`= 99/100`

Khi đó: 

`A = C + B = 100 . 1 + 99/100 = 100 + 99/100 = 10099/100`

Dãy số lập được là: 

`4;9;14;19;...;1544`

Số số hạng có trong dãy số là: 

`(1544 - 4) : 5 + 1 = 309` (số hạng)

Tổng của các số hạng trong dãy số là: 

`(1544 + 4) . 309 : 2 = 239166` 

Vậy ...

Dãy các số theo yêu cầu đề bài là:

4; 9; 14; ...; 1544

Quy luật: 2 số liền nhau cách nhau 5 đơn vị.

Số số hạng của dãy là: (1544 - 4) : 5 + 1 = 309 (số)

Tổng các số từ 4 - 1544 là: (4 + 1544) x 309 : 2 = 239166

Đáp số: 239166

Vì là ước không bắt buộc là só nguyên tố nên các ước lớn hơn  của 30 là: 10; 15; 30.

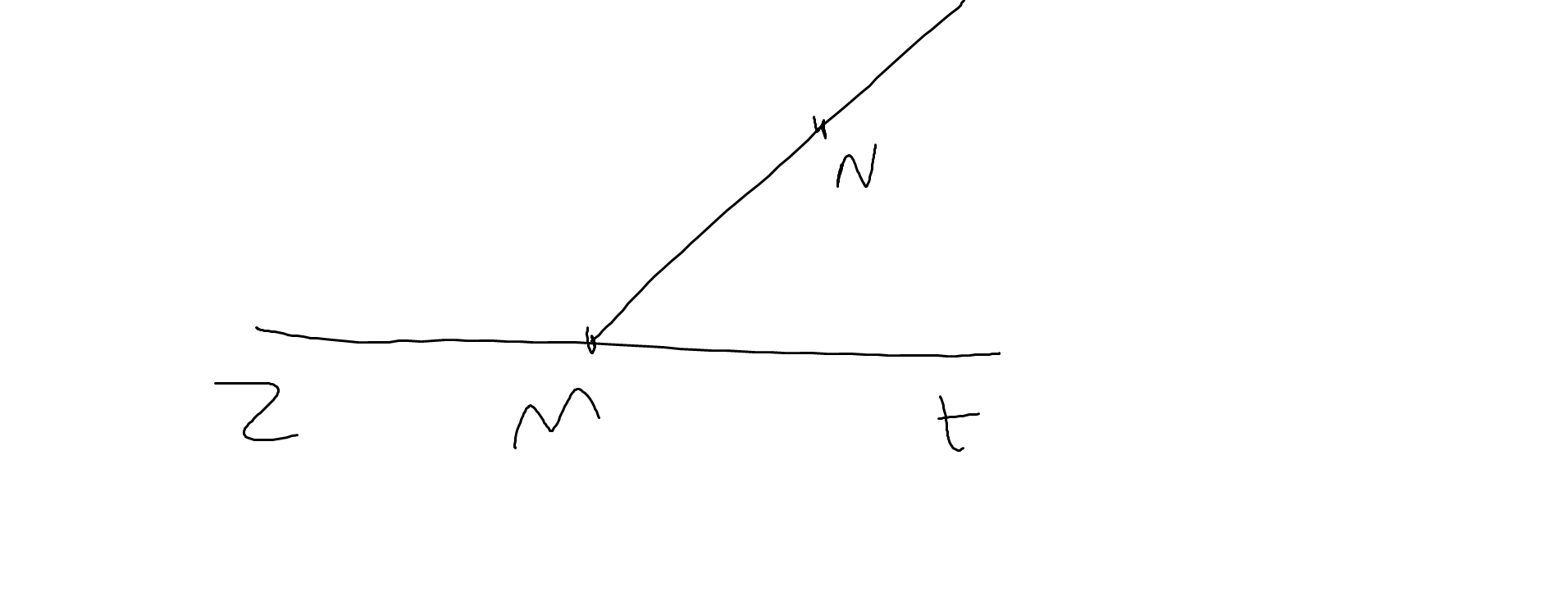
a: Các góc có trong hình vẽ là \(\widehat{tMN};\widehat{zMN};\widehat{tMz}\)

b: Góc bẹt là \(\widehat{tMz}\)

Gọi d là ƯCLN của `2n+3` và `4n+7`

Ta có: 

`2n+3` ⋮ d và `4n+7` ⋮ d 

`=>2(2n+3)` ⋮ d và `4n+7` ⋮ d

`=>4n+6` ⋮ d và `4n+7` ⋮ d 

`=>(4n+7)-(4n+6)` ⋮ d 

`=>1` ⋮ d 

`=>d=1` 

Vậy: `2n+3` và `4n+7` là 2 số nguyên tố cùng nhau 

Mọi người giúp em với ạ, bây giờ em đang cần gấp ạ!

x.16 - x.4 - x = 2

x. (16 - 4 - 1) = 2

x.       11        = 2

x                    = 2. 11

                  x = 22

           Vậy x = 22

x.16 - x.4 - x = 2

x.(16-4-1) = 2

x.11 = 2

x = 2:11

x = \(\dfrac{2}{11}\)

\(5^{2x-1}=125\\ =>5^{2x-1}=5^3\\ =>2x-1=3\\ =>2x=3+1\\ =>2x=4\\ =>x=\dfrac{4}{2}\\ =>x=2\)

Vậy: ... 

5^{2x - 1} = 125

5^{2x - 1} = 5³

2x - 1 = 3

2x      = 3 +1

2x      = 4

  x      = 4 :2

  x      = 2

\(P=\dfrac{\left(x-1\right)^2+3}{\left(x-1\right)^2+5}=\dfrac{\left(x-1\right)^2+5-2}{\left(x-1\right)^2+5}=1-\dfrac{2}{\left(x-1\right)^2+5}\)

\(\left(x-1\right)^2+5>=5\forall x\)

=>\(\dfrac{2}{\left(x-1\right)^2+5}< =\dfrac{2}{5}\forall x\)

=>\(-\dfrac{2}{\left(x-1\right)^2+5}>=-\dfrac{2}{5}\forall x\)

=>\(P=\dfrac{-2}{\left(x-1\right)^2+5}+1>=-\dfrac{2}{5}+1=\dfrac{3}{5}\forall x\)

Dấu '=' xảy ra khi x-1=0

=>x=1

\(Q=\dfrac{\left(2y+3\right)^2-3}{\left(2y+3\right)^2+4}=\dfrac{\left(2y+3\right)^2+4-7}{\left(2y+3\right)^2+4}=1-\dfrac{7}{\left(2y+3\right)^2+4}\)

\(\left(2y+3\right)^2+4>=4\forall y\)

=>\(\dfrac{7}{\left(2y+3\right)^2+4}< =\dfrac{7}{4}\forall y\)

=>\(-\dfrac{7}{\left(2y+3\right)^2+4}>=-\dfrac{7}{4}\forall y\)

=>\(Q=-\dfrac{7}{\left(2y+3\right)^2+4}+1>=-\dfrac{3}{4}\forall y\)

Dấu '=' xảy ra khi 2y+3=0

=>2y=-3

=>y=-3/2

\(F=\dfrac{\left(x-1\right)^2+5}{\left(x-1\right)^2+2}=\dfrac{\left(x-1\right)^2+2+3}{\left(x-1\right)^2+2}=1+\dfrac{3}{\left(x-1\right)^2+2}\)

\(\left(x-1\right)^2+2>=2\forall x\)

=>\(\dfrac{3}{\left(x-1\right)^2+2}< =\dfrac{3}{2}\forall x\)

=>\(F=\dfrac{3}{\left(x-1\right)^2+2}+1< =\dfrac{5}{2}\forall x\)

Dấu '=' xảy ra khi x-1=0

=>x=1

\(2^{x+2}+2^{x+2}+2^{x+1}=224\\ =>2^{x+1}\cdot2+2^{x+1}\cdot2+2^{x+1}\cdot1=224\\ =>2^{x+1}\cdot\left(2+2+1\right)=224\\ =>2^{x+1}\cdot5=224\\ =>2^{x+1}=\dfrac{224}{5}\\ =>x+1=log_2\dfrac{224}{5}\\ =>x=log_2\dfrac{224}{5}-1\)

Gọi tổng số học sinh giỏi lớp 6;7;8 là x

Do x chia 3 dư 2, chia 4 dư 3, chia 53 dư 52

\(\Rightarrow x+1\) chia hết cho 3,4,53

\(\Rightarrow x+1\in BC\left(3;4;53\right)\)

Mà x nhỏ nhất 

\(\Rightarrow x+1=BCNN\left(3;4;53\right)\)

\(\Rightarrow x+1=636\)

\(\Rightarrow x=635\)

mọi người giúp e với bây giờ e đang gấp ạ!