Viết 1 bài văn trò chơi điện tử mang lại lợi ích hay hại cho học sinh (ngắn gọn)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)

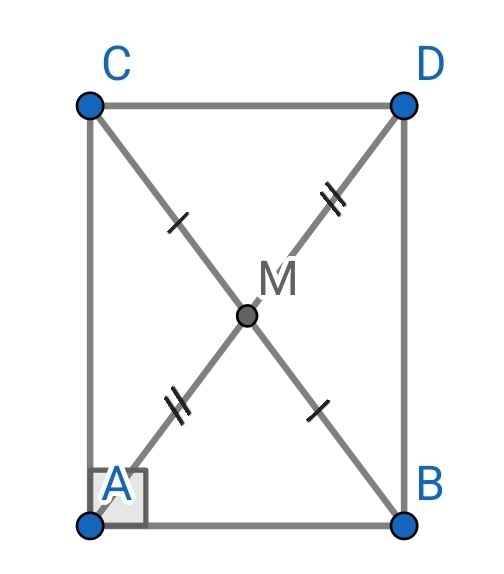
xét 2 tam giác AMB và DMC
có AM = DM ( gt )
góc DMC = góc AMB ( 2 góc đối đỉnh )
BM = CM ( M là trung điểm của BC )
=> tam giác AMB = tam giác DMC ( c.g.c ) ( đpcm )
b, xét hai tam giác AMC và DMB
có AM = DM ( gt )
góc DMB = góc AMC ( 2 góc đối đỉnh )
BM = CM ( M là trung điểm của BC )
=> tam giác AMC = ta giác DMB ( c.g.c )
=> góc DBM = góc ACM ( 2 góc tương ứng )
mà 2 góc trên nằm ở vị trí so le trong của 2 đt AC và BD
=> AC // BD ( đpcm )
c, từ b có
tam giác AMC = tam giác DMB ( c.g.c )
=> AC = BD ( 2 cạnh tương ứng )
và góc DBM = góc ACM ( 2 góc tương ứng )
xét hai tam giác AKC và BHD
có góc BHD = góc CKA = 90 độ
AC = BD (cmt)
góc DBM = góc ACM ( cmt )
=> tam giác AKC = tam giác BHD ( cạnh huyền - govs nhọn )
=> BH = CK ( 2 cạnh tương ứng )(đpcm )

 a) Do M là trung điểm của BC (gt)
a) Do M là trung điểm của BC (gt)
⇒ MB = MC
Xét ∆MAB và ∆MDC có:
MA = MD (gt)
∠AMB = ∠DMC (đối đỉnh)
MB = MC (cmt)
⇒ ∆MAB = ∆MDC (c-g-c)
b) Do ∆MAB = ∆MDC (cmt)
⇒ ∠MAB = ∠MDC (hai góc tương ứng)
Mà ∠MAB và ∠MDC là hai góc so le trong
⇒ AB // CD
c) Do MA = MD (gt)
⇒ AD = 2AM
Do ∆ABC vuông tại A (gt)
⇒ AB ⊥ AC
Mà AB // CD (cmt)
⇒ CD ⊥ AC
⇒ ∆CDA vuông tại C
Do ∆MAB = ∆MDC (cmt)
⇒ AB = CD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ABC và ∆CDA có:
AC là cạnh chung
AB = CD (cmt)
⇒ ∆ABC = ∆CDA (hai cạnh góc vuông)
⇒ BC = AD (hai cạnh tương ứng)
Mà AD = 2AM (cmt)
⇒ BC = 2AM
d) Xét ∆MAC và ∆MDB có:
MA = MD (gt)
∠AMC = ∠DMB (đối đỉnh)
MC = MB (cmt)
⇒ ∆MAC = ∆MDB (c-g-c)
⇒ ∠MAC = ∠MDB (hai góc tương ứng)
Mà ∠MAC và ∠MDB là hai góc so le trong
⇒ AC // BD
Mà AC ⊥ AB (cmt)
⇒ AB ⊥ BD

21.x = 19.y và x-y=4
Hay x/21 = y/19 và x - y = 4
Áp dụng tính chất của dãy tỉ số bằng nhau ta có
x/21 = y/19 = x-y/21-19 = 4/2 = 2
=> x/21 = 2 => x = -2 × 19 = 42
y/19 = 2 => y = -2 × 22 = 38
Vậy x = 42
y = 38

Câu 1: Phương thức biểu đạt chính là: Biểu cảm
Bài thơ sử dụng thể thơ lục bát.
Câu 2: Dấu chấm lửng ở câu thơ đầu tỏ ý còn nhiều sự vật, hiện tượng chưa được liệt kê khác. Bên cạnh đó có thể hiểu dấu ba chấm là tiếng ngân dài trong câu hát của người mẹ.
Câu 3: Biện pháp tu từ nhân hóa "trái hồng trái bưởi đánh đu ngày rằm" kết hợp cùng biện pháp điệp cấu trúc "Bao giờ cho đến..."
Tác dụng:
- Tăng tính biểu hình biểu đạt gây ấn tượng sâu sắc với người đọc.
- Khơi gợi khát khao thời thơ ấu với những hình ảnh quen thuộc
- Tô đậm tình cảm của tác giả đối với hồi ức tuổi thơ của mình.
Câu 4: Đoạn thơ trên gửi tới chúng ta thông điệp: ghi nhớ công lao chăm sóc dưỡng dục trời bể của mẹ. Chúng ta cần sống sao cho tròn đạo hiếu, đối xử thật tốt với mẹ đừng khiến mẹ phải buồn hay lo lắng về chúng ta.
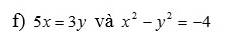
what có nữa luôn hả
???