Cho biểu đồ.
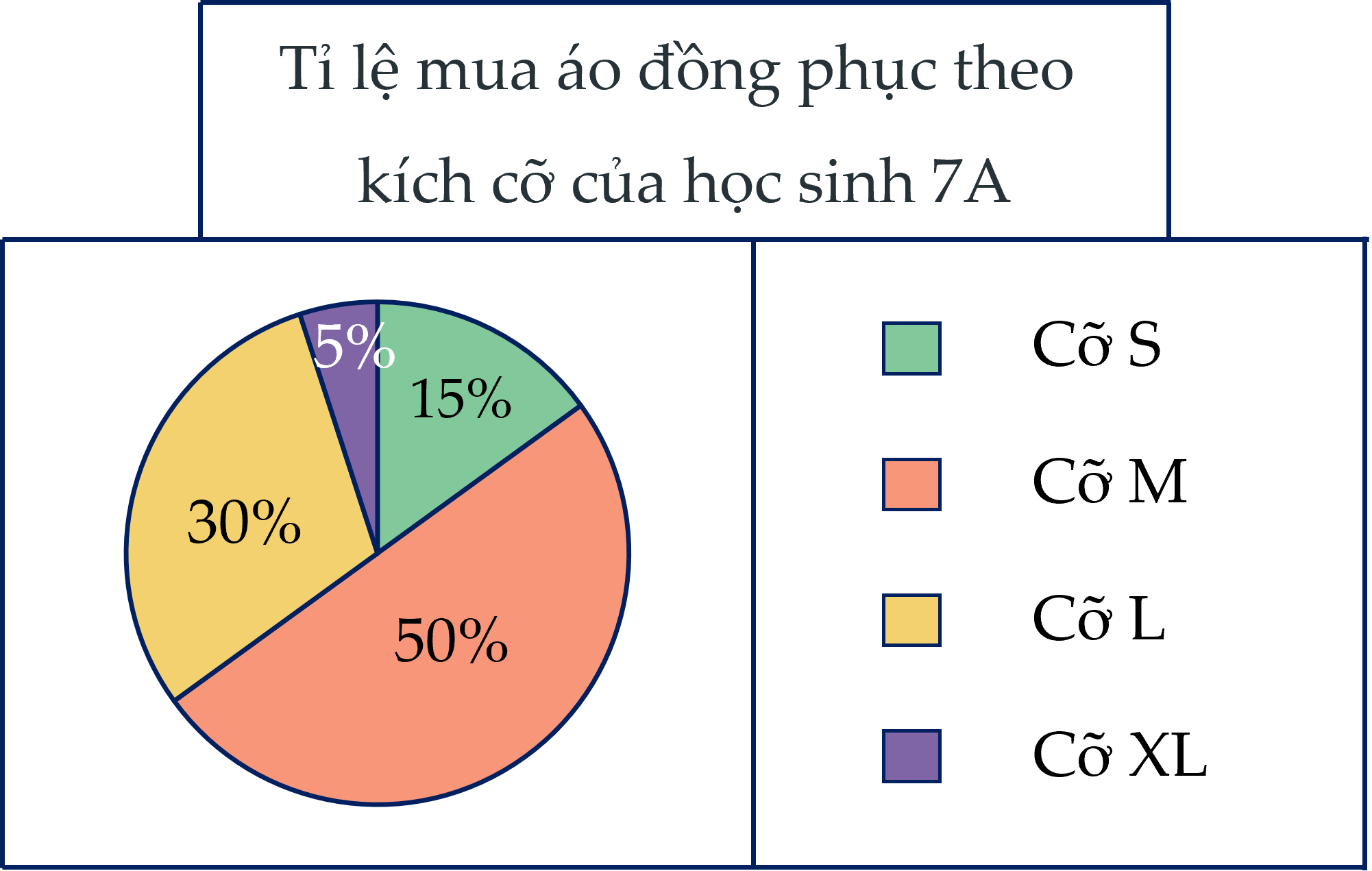
Quan sát biểu đồ quạt tròn trên, em hãy cho biết:
a) Cỡ áo nào có tỉ lệ học sinh đặt mua nhiều nhất?
b) Cỡ áo nào có tỉ lệ học sinh đặt mua ít nhất?
c) Biết lớp 7A có 40 học sinh. Tính số lượng bạn đã mua áo đồng phục mỗi loại.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

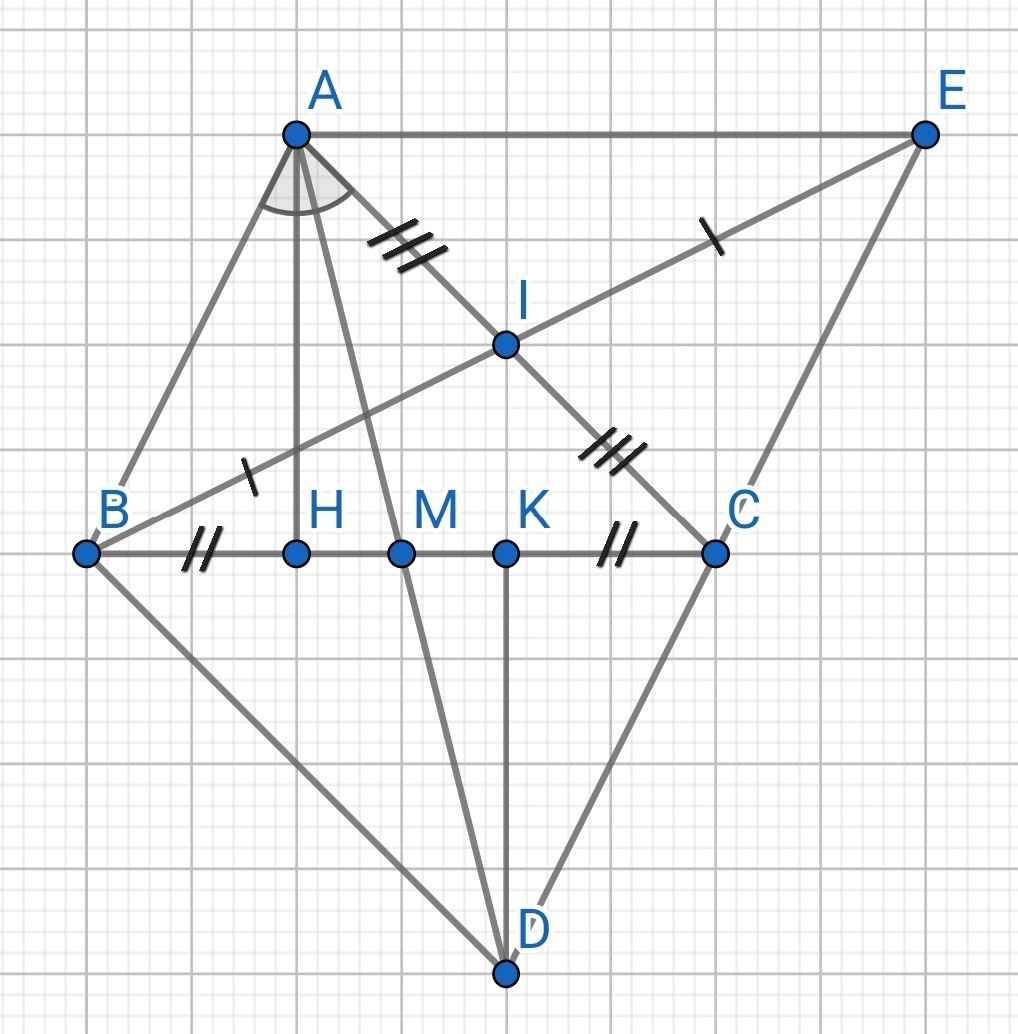 c) Do M là trung điểm của BC (gt)
c) Do M là trung điểm của BC (gt)
⇒ BM = MC
Xét hai tam giác vuông: ∆AHM và ∆DKM có:
MA = MD (gt)
∠AMH = ∠DMK (đối đỉnh)
⇒ ∆AHM = ∆DKM (cạnh huyền - góc nhọn)
⇒ HM = KM (hai cạnh tương ứng)
Ta có:
BK = BM + KM
CH = CM + HM
Mà BM = CM (cmt)
KM = HM (cmt)
⇒ BK = CH
d) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
⇒ AB // DC và AB = DC
Tứ giác ABCE có:
I là trung điểm của AC (gt)
I là trung điểm của BE (gt)
⇒ ABCE là hình bình hành
⇒ AB // CE và AB = CE
Do AB // CE (cmt)
AB // DC (cmt)
⇒ C, D, E thẳng hàng (theo tiên đề Ơ-clít)
Ta có:
AB = CE (cmt)
AB = DC (cmt)
⇒ CD = CE
⇒ C là trung điểm của DE

a/
Ta có
\(\widehat{EAD}=\widehat{BAI}\) (góc đối dỉnh)
\(\widehat{IAC}=\widehat{BAI}\left(gt\right)\)
\(\Rightarrow\widehat{EAD}=\widehat{IAC}\)
Xét tg EAD và tg IAC có
\(\widehat{EAD}=\widehat{IAC}\left(cmt\right)\)
AE=AI (gt); AD=AC (gt)
=> tg EAD = tg IAC (c.g.c)\(\Rightarrow\widehat{ADE}=\widehat{ACI}\)
b/
Xét tg ACD có
AD=AC (gt) => tg ACD cân tại A
Ta có
MD=MC (gt)
\(\Rightarrow\widehat{MAD}=\widehat{MAC}\) (trong tg cân đường trung tuyến xuất phát từ đỉnh tg cân đồng thời là đường phân giác của góc ở đỉnh tg cân)
Ta có
tg EAD = tg IAC (cmt) \(\Rightarrow\widehat{EAD}=\widehat{IAC}\)
\(\Rightarrow\widehat{MAD}+\widehat{EAD}=\widehat{MAC}+\widehat{IAC}\)
\(\Rightarrow\widehat{MAE}=\widehat{MAI}\)
Mà \(\widehat{MAE}+\widehat{MAI}=\widehat{EAI}=180^o\Rightarrow\widehat{MAE}=\widehat{MAI}=90^o\Rightarrow AM\perp AI\)
c/
\(AM\perp AI\Rightarrow AM\perp IE\) (1)
Xét tg cân ACD có
MD=MC (gt)
\(\Rightarrow AM\perp CD\) (trong tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao) (2)
Từ (1) và (2) => IE//CD (cùng vuông góc với AM)

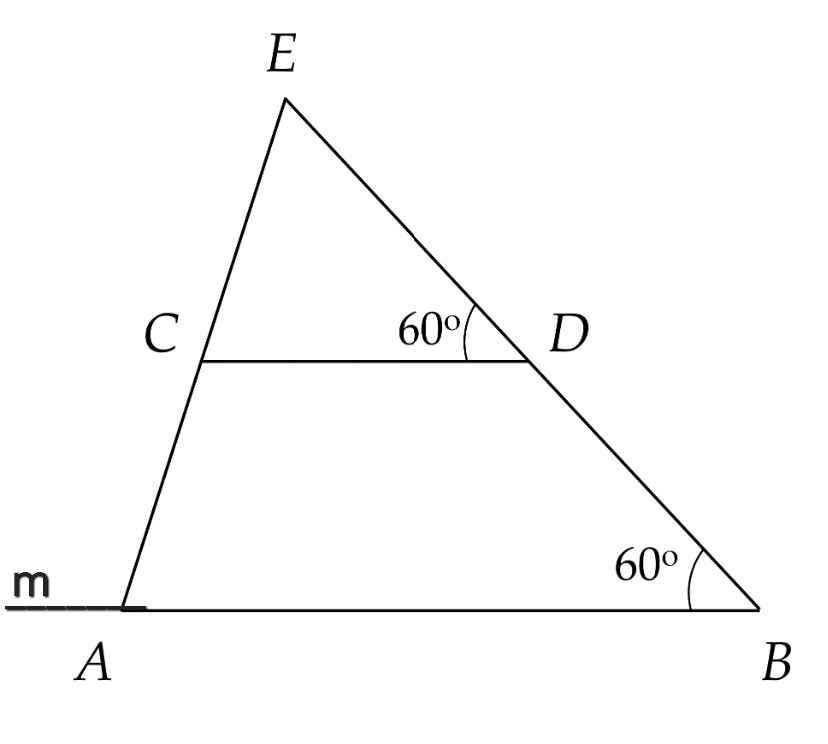
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰

2/3 - |x - 1/2| = 2/3
|x - 1/2| = 2/3 - 2/3
|x - 1/2| = 0
x - 1/2 = 0
x = 0 + 1/2
x = 1/2

11/3 . 2/5 + 11/3 . 8/5 - 11/3
= 11/3 . (2/5 + 8/5 - 1)
= 11/3 . (2 - 1)
= 11/3 . 1
= 11/3


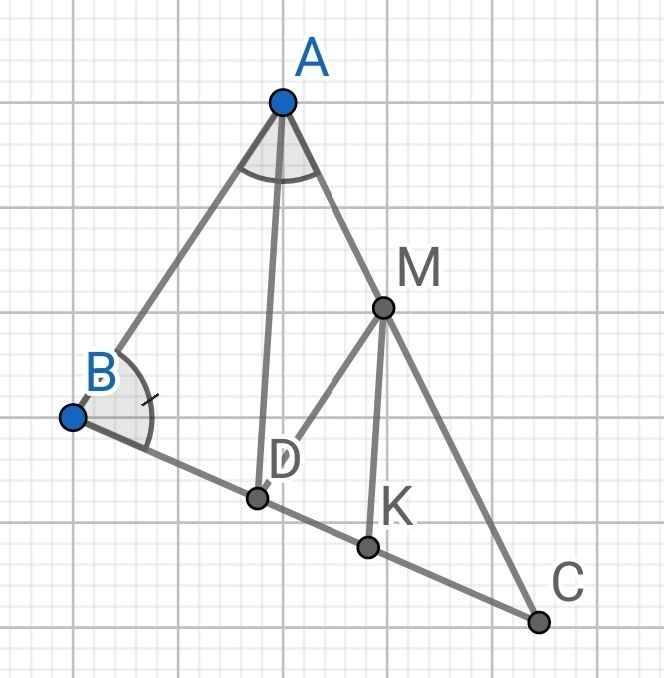
Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠DAM = 60⁰ : 2 = 30⁰
Do DM // AB (gt)
⇒ ∠ADM = ∠BAD = 30⁰ (so le trong)
Do DM // AB (gt)
⇒ ∠MDK = ∠B = 80⁰ (đồng vị)
⇒ ∠ADK = ∠ADM + ∠MDK
= 30⁰ + 80⁰
= 110⁰

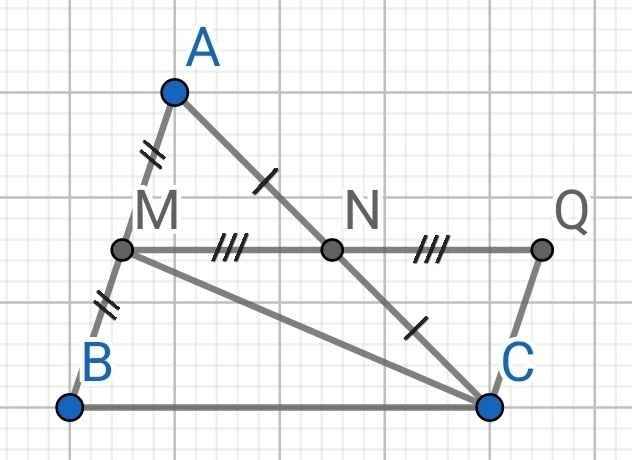
a) Xét ∆AMN và ∆CQN có:
AN = NC (do N là trung điểm của AC)
∠ANM = ∠CNQ (đối đỉnh)
NM = NQ (gt)
⇒ ∆AMN = ∆CQN (c-g-c)
b) Do ∆AMN = ∆CQN (cmt)
⇒ ∠MAN = ∠NCQ (hai góc tương ứng)
Mà ∠MAN và ∠NCQ là hai góc so le trong
⇒ AM // CQ
⇒ MB // CQ
c) Do ∆AMN = ∆CQN (cmt)
⇒ AM = CQ (hai cạnh tương ứng)
Mà AM = MB (do M là trung điểm của AB)
⇒ MB = CQ
Do BM // CQ (cmt)
⇒ ∠BMC = ∠QCM (so le trong)
Xét ∆BMC và ∆QCM có:
BM = CQ (cmt)
∠BMC = ∠QCM (cmt)
CM là cạnh chung
⇒ ∆BMC = ∆QCM (c-g-c)
⇒ BC = MQ (hai cạnh tương ứng)
Do NM = NQ (gt)
⇒ MN = 1/2 MQ
Mà BC = MQ (cmt)
⇒ MN = 1/2 BC
a) Cỡ áo nào có tỉ lệ học sinh đặt mua nhiều nhất? -> Cỡ M
b) Cỡ áo nào có tỉ lệ học sinh đặt mua ít nhất? -> Cỡ XL
c) Biết lớp 7A có 40 học sinh. Tính số lượng bạn đã mua áo đồng phục mỗi loại.
Số bạn mua áo cỡ S:
\(15\%.40=6\left(HS\right)\)
Số bạn mua áo cỡ M:
\(50\%.40=20\left(HS\right)\)
Số bạn mua áo cỡ L:
\(30\%.40=12\left(HS\right)\)
Số bạn mua áo cỡ XL:
\(5\%.40=2\left(HS\right)\)
Đ.số:.......