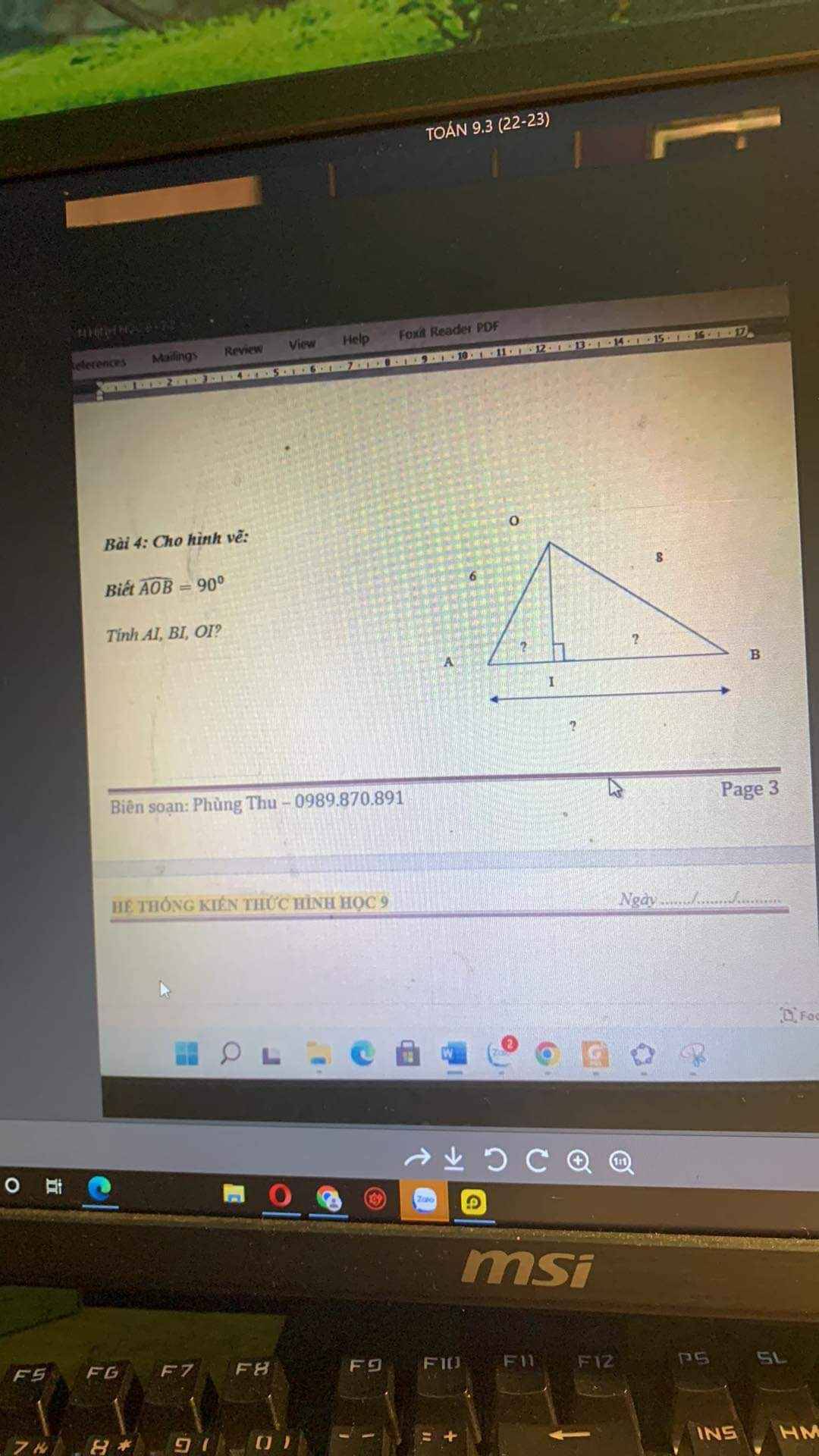
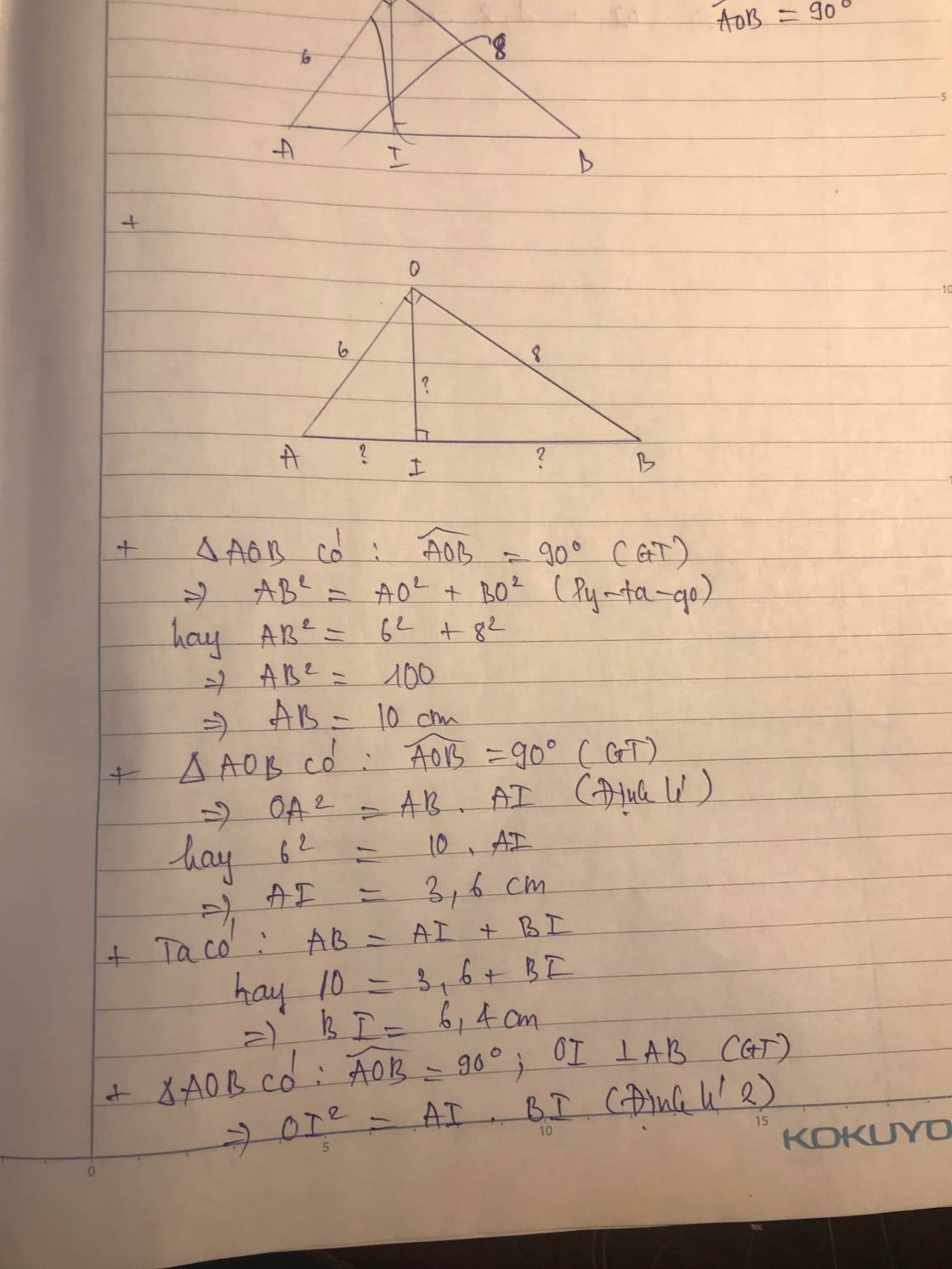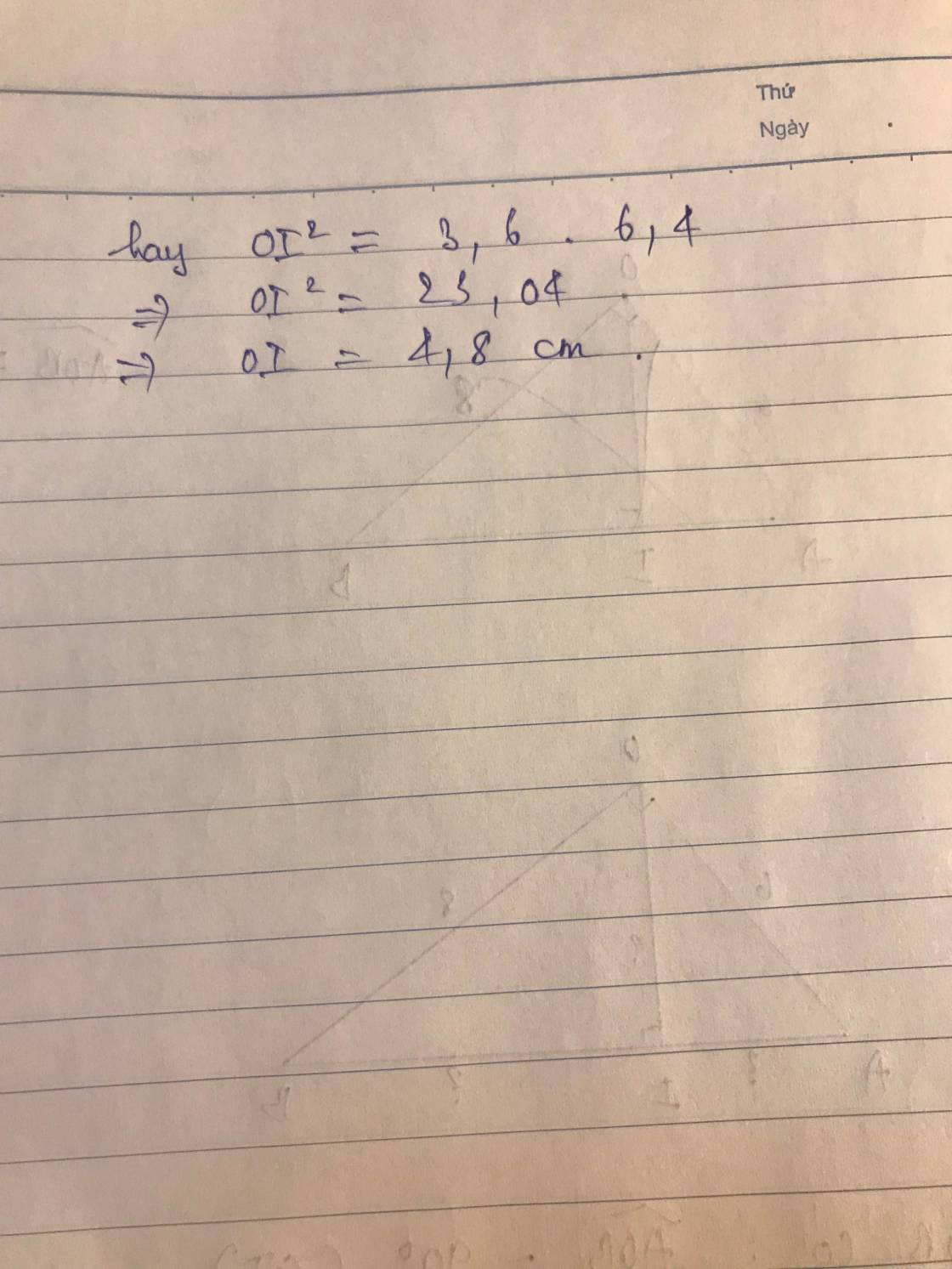trong bài mxnn mọi người thấy khổ nào là quan trọng và có thể cho thi ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ tiếp tuyến Ax của đường tròn (O).
Trong tam giác ABH vuông tại H có đường cao HE nên ta có \(AH^2=AE.AB\)
Tương tự, ta cũng có \(AH^2=AF.AC\), từ đó suy ra \(AE.AB=AF.AC\) hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ACB\) có \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\left(cmt\right)\) và \(\widehat{A}\) chung
\(\Rightarrow\Delta AEF~\Delta ACB\left(c.g.c\right)\) \(\Rightarrow\widehat{AEF}=\widehat{ACB}\) (1)
Mặt khác, trong đường tròn (O) có \(\widehat{BAx}\) và \(\widehat{ACB}\) lần lượt là góc tạo bởi tiếp tuyến và dây cung, và góc nội tiếp cùng chắn \(\stackrel\frown{AB}\) nên ta có \(\widehat{BAx}=\widehat{ACB}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{AEF}=\widehat{BAx}\) \(\Rightarrow EF//Ax\) (2 góc so le trong bằng nhau)
Lại có Ax là tiếp tuyến tại A của (O) nên \(Ax\perp OA\) tại A, dẫn đến \(OA\perp EF\) (đpcm)

a)
| CTHH | Phân loại |
| K2O | Oxit bazo |
| MgO | Oxit bazo |
| SO2 | Oxit axit |
| CaO | Oxit bazo |
| CO2 | Oxit axit |
| N2O | Oxit trung tính |
| N2O5 | Oxit axit |
| Fe2O3 | Oxit bazo |
| P2O5 | Oxit axit |
| SO2 (ở trên có rồi nhé :) |
b)
\(K_2O+H_2O\rightarrow2KOH\)
\(SO_2+H_2O\rightarrow H_2SO_3\)
\(CaO+H_2O\rightarrow Ca\left(OH\right)_2\)
\(CO_2+H_2O\rightarrow H_2CO_3\)
\(N_2O_5+H_2O\rightarrow2HNO_3\)
\(P_2O_5+3H_2O\rightarrow2H_3PO_4\)
c)
\(K_2O+2HCl\rightarrow2KCl+H_2O\)
\(MgO+2HCl\rightarrow MgCl_2+H_2O\)
\(CaO+2HCl\rightarrow CaCl_2+H_2O\)
\(Fe_2O_3+6HCl\rightarrow2FeCl_3+3H_2O\)
d)
\(2NaOH+SO_2\rightarrow Na_2SO_3+H_2O\)
\(2NaOH+CO_2\rightarrow Na_2CO_3+H_2O\)
\(2NaOH+N_2O_5\rightarrow2NaNO_3+H_2O\)
\(6NaOH+P_2O_5\rightarrow2Na_3PO_4+3H_2O\)
- Có các oxit không tác dụng với NaOH nhưng tác dụng với nước trong dung dịch:
\(K_2O+H_2O\rightarrow2KOH\)
\(CaO+H_2O\rightarrow Ca\left(OH\right)_2\)


a) Ta có :
VT : \(\dfrac{\left(x\sqrt{y}+y\sqrt{x}\right)\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{xy}}\)
\(=\dfrac{\left(\sqrt{x^2y}+\sqrt{xy^2}\right)\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{xy}}\)
\(=\dfrac{\sqrt{xy}\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)}{\sqrt{xy}}=\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}\right)\)
\(=\left(\sqrt{x}\right)^2-\left(\sqrt{y}\right)^2=x-y\) với \(x>0;y>0\)
VT\(=\)VP nên đẳng thức được chứng minh.
b) Vì \(x>0\) nên \(\sqrt{x^3}=\left(\sqrt{x}\right)^3\)
Ta có :
VT \(\dfrac{\sqrt{x^3}-1}{\sqrt{x}-1}=\dfrac{\left(\sqrt{x}\right)^3-1^3}{\sqrt{x}-1}=\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=x+\sqrt{x}+1\) với \(x\ge0;x\ne1\)
VT\(=\)VP nên đẳng thức được chứng minh.

\(\dfrac{1}{x-1}+\dfrac{6}{3x+5}=\dfrac{2}{x+2}+\dfrac{1}{x+3}\) (ĐK: \(x\notin\left\{1,-\dfrac{5}{3},-2,-3\right\}\))
\(\Rightarrow\left(3x+5\right)\left(x+2\right)\left(x+3\right)+6\left(x-1\right)\left(x+2\right)\left(x+3\right)=2\left(x-1\right)\left(3x+5\right)\left(x+3\right)+\left(x-1\right)\left(3x+5\right)\left(x+2\right)\)
\(\Leftrightarrow7x^2+24x+17=0\)
\(\Leftrightarrow\left(7x+17\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-17}{7}\\x=-1\end{matrix}\right.\) (thỏa mãn)

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn!

\(\Leftrightarrow\left\{{}\begin{matrix}2x^2+4x+y^3+3=0\\x^2y^3+y=2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x^2+2\left(x^2y^3+y\right)+y^3+3=0\left(1\right)\\x^2y^3+y=2x\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow2x^2+2x^2y^3+2y+y^3+3=0\Leftrightarrow\left(y+1\right)\left(2x^2y^2-2x^2y+y^2+2x-y+3\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-1\Rightarrow x=-1\\2x^2y^2-2x^2y+y^2+2x^2-y+3=0\left(3\right)\end{matrix}\right.\)
\(\left(3\right)\Leftrightarrow2x^2\left(y^2-y+2\right)+y^2-y+3=0\)
\(\Rightarrow a=y^2-y+2=\left(y-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
\(\Delta=0-4.2\left(y^2-y+2\right)\left(y^2-y+3\right)=-8\left(y^2-y+2\right)\left(y^2-y+3\right)\)
\(y^2-y+3=\left(y-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\)
\(\Rightarrow\Delta=-8\left(y^2-y+2\right)\left(y^2-y+3\right)< 0\)
\(\Rightarrow\left(3\right)\) không tồn tại nghiệm (x;y) nào
do đó hpt có nghiệm x=y=-1

Lời giải:
ĐKXĐ: $x\neq -1$
PT $\Leftrightarrow (x-\frac{x}{x+1})^2+4=\frac{5x^2}{x+1}$
$\Leftrightarrow (\frac{x^2}{x+1})^2+4=\frac{5x^2}{x+1}$
Đặt $\frac{x^2}{x+1}=a$ thì pt trở thành:
$a^2+4=5a$
$\Leftrightarrow (a-1)(a-4)=0$
$\Leftrightarrow a=1$ hoặc $a=4$
Nếu $a=1\Leftrightarrow \frac{x^2}{x+1}=1$
$\Rightarrow x^2-x-1=0$
$\Leftrightarrow x=\frac{1\pm \sqrt{5}}{2}$
Nếu $a=4\Leftrightarrow \frac{x^2}{x+1}=4$
$\Rightarrow x^2-4x-4=0$
$\Leftrightarrow x=2\pm 2\sqrt{2}$