\(\dfrac{11}{12}x+0,25=\dfrac{5}{6}\\ \dfrac{11}{12}x=\dfrac{5}{6}-\dfrac{1}{4}=\dfrac{7}{12}\\ x=\dfrac{7}{12}:\dfrac{11}{12}=\dfrac{7}{11}\)

không nhé như hình (hình 2) này trong cùng phía là N2 và M4.

Hình 1 có 2 góc zOy và góc xOy là 2 góc kề bù và có tổng 180 độ

KO

Một số mặt hàng xuất khẩu và nhập khẩu của Việt Nam với Liên minh Châu Âu là: Gạo; Hạt tiêu; Cà phê; Cao su; Chè; Hạt điều; Mặt hàng gỗ và các sản phẩm gỗ; Mặt hàng dệt may;...

Thể tích bể bơi:

2 x 1 x 0,5 = 1 (m³) = 1000 (dm³)= 1000 (lít)

Lượng nước bơm vào bể trong 30 phút:

20 x 30 = 600 (lít)

Hiện tại bể có:

600 + 60 = 660 (lít) < 1 000 (lít)

Nên bể chưa đầy nước

Thể tích bể:

2 × 1 × 0,5 = 1 (m³) = 1000 (l)

Số lít nước đã bơm vào bể sau 30 phút:

30 × 20 = 600 (l)

Tổng số lít nước trong bể:

600 + 60 = 660(l)

Do 1000 > 660 nên bể chưa đầy nước

Bài 3:

\(a,A=x^2-x=\left(x^2-2.x.\dfrac{1}{2}+\dfrac{1}{4}\right)-\dfrac{1}{4}=\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge\dfrac{1}{4}\forall x\in R\\ Vậy:min_A=\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{2}\)

\(b,B=2x^2-8x=2\left(x^2-x\right)=2\left(x^2-2.x.\dfrac{1}{2}+\dfrac{1}{4}\right)-\dfrac{1}{2}=2.\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{2}\forall x\in R\\ Vậy:min_B=\dfrac{1}{2}\Leftrightarrow x=\dfrac{1}{2}\)

\(c,C=3x^2-12x=3\left(x^2-x\right)=3\left(x^2-2.x.\dfrac{1}{2}+\dfrac{1}{4}\right)-\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2-\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\in R\\ Vậy:min_C=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)

Câu trên có ý nghĩa: cho thấy niềm vui và hạnh phúc của tác giả khi mùa xuân của đất trời đang đến cận kề. Mùa xuân tới không chỉ mang đến sức sống rạo rực cho thiên nhiên mà còn cả sức sống mãnh liệt trỗi dậy trong tâm hồn con người. Qua đó ta thấy tình yêu sâu sắc của tác giả dành cho mùa xuân nói riêng và thiên nhiên đất trời nói chung.

Lời giải:

Gọi tiền lãi ba đơn vị nhận được lần lượt là: $a,b,c$ (triệu đồng) 

Theo bài ra ta có: $\frac{a}{3}=\frac{b}{4}=\frac{c}{7}$ và $a+b+c=980$

Áp dụng TCDTSBN:

$\frac{a}{3}=\frac{b}{4}=\frac{c}{7}=\frac{a+b+c}{3+4+7}=\frac{980}{14}=70$

$\Rightarrow a=70.3=210$ (triệu đồng); $b=70.4=280$ (triệu đồng); $c=70.7=490$ (triệu đồng)

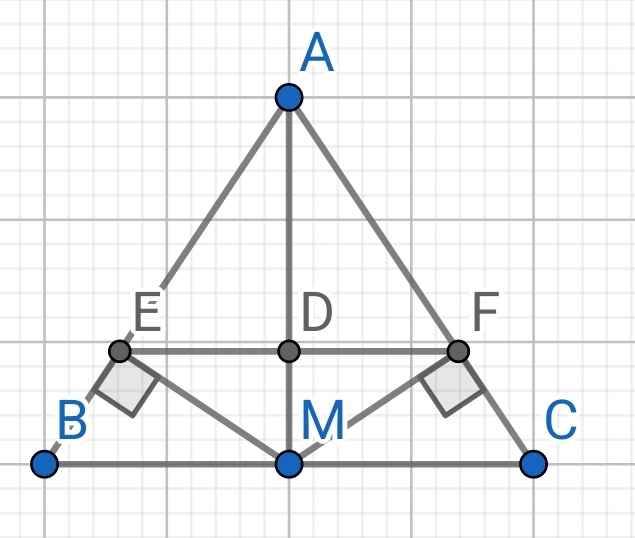 a) Do M là trung điểm của BC (gt)

⇒ BM = CM

Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét ∆AMB và ∆AMC có:

AM là cạnh chung

AB = AC (cmt)

BM = CM (cmt)

⇒ ∆AMB = ∆AMC (c-c-c)

b) Sửa đề:

Chứng minh AM EF

Giải:

Gọi D là giao điểm của AM và EF

Do ∆AMB = ∆AMC (cmt)

⇒ ∠MAB = ∠MAC (hai góc tương ứng)

⇒ ∠MAE = ∠MAF

Xét hai tam giác vuông: ∆MAE và ∆MAF có:

AM là cạnh chung

∠MAE = ∠MAF (cmt)

⇒ ∆MAE = ∆MAF (cạnh huyền - góc nhọn)

⇒ AE = AF (hai cạnh tương ứng)

Do ∠MAE = ∠MAF (cmt)

⇒ ∠DAE = ∠DAF 

Xét ∆ADE và ∆ADF có:

AD là cạnh chung

∠DAE = ∠DAF (cmt)

AE = AF (cmt)

⇒ ∆ADE = ∆ADF (c-g-c)

⇒ ∠ADE = ∠ADF (hai góc tương ứng)

Mà ∠ADE + ∠ADF = 180⁰ (kề bù)

⇒ ∠ADE = ∠ADF = 180⁰ : 2 = 90⁰

⇒ AD ⊥ EF

.

a/

Xét tg MAB và tg MEC có

MB=MC (gt); MA=ME (gt)

\(\widehat{AMB}=\widehat{EMC}\) (góc đối đỉnh)

=> tg MAB = tg MEC (c.g.c)

b/

Ta có  tg MAB = tg MEC (cmt) \(\Rightarrow\widehat{BAM}=\widehat{CEM}\) 

Hai góc trên ở vị trí so le trong => AB//CE

c/

Xét tg vuông ABH và tg vuông DBH có

HA=HD (gt); BH chung => tg ABH = tg DBH (hai tg vuông có 2 cạnh góc vuông bằng nhau) => AB=BD(1)

Ta có tg MAB = tg MEC (cmt) => AB=CE (2)

Từ (1) và (2) => BD=CE

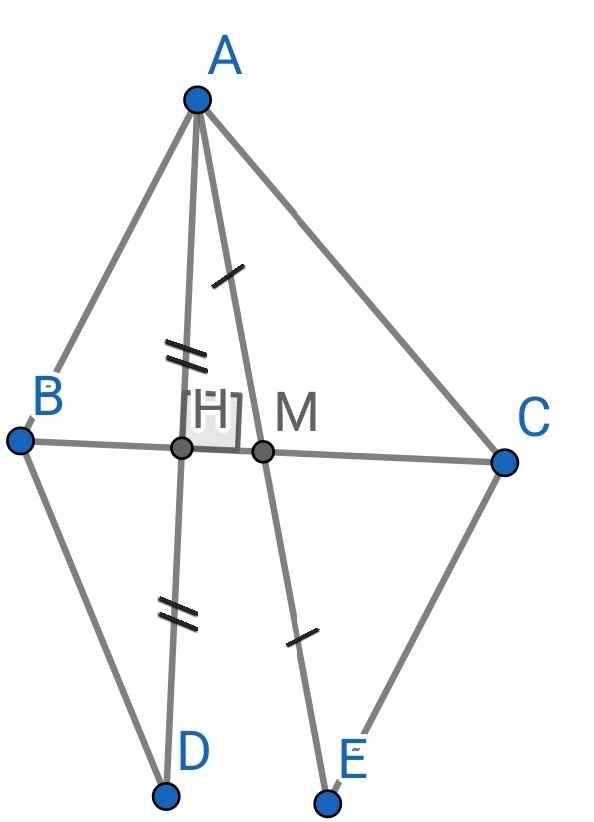 a) Do M là trung điểm của BC (gt)

⇒ BM = MC

Xét ∆MAB và ∆MEC có:

BM = MC (cmt)

∠AMB = ∠EMC (đối đỉnh)

AM = ME (gt)

⇒ ∆MAB = ∆MEC (c-g-c)

b) Do ∆MAB = ∆MEC (cmt)

⇒ ∠MAB = ∠MEC (hai góc tương ứng)

Mà ∠MAB và ∠MEC là hai góc so le trong)

AB // CE

c) Xét hai tam giác vuông: ∆AHB và ∆DHB có:

BH là cạnh chung

AH = HD (gt)

⇒ ∆AHB = ∆DHB (hai cạnh góc vuông)

⇒ AB = BD (hai cạnh tương ứng)

Do ∆MAB = ∆MEC (cmt)

⇒ AB = CE (hai cạnh tương ứng)

Mà AB = BD (cmt)

⇒ BD = CE