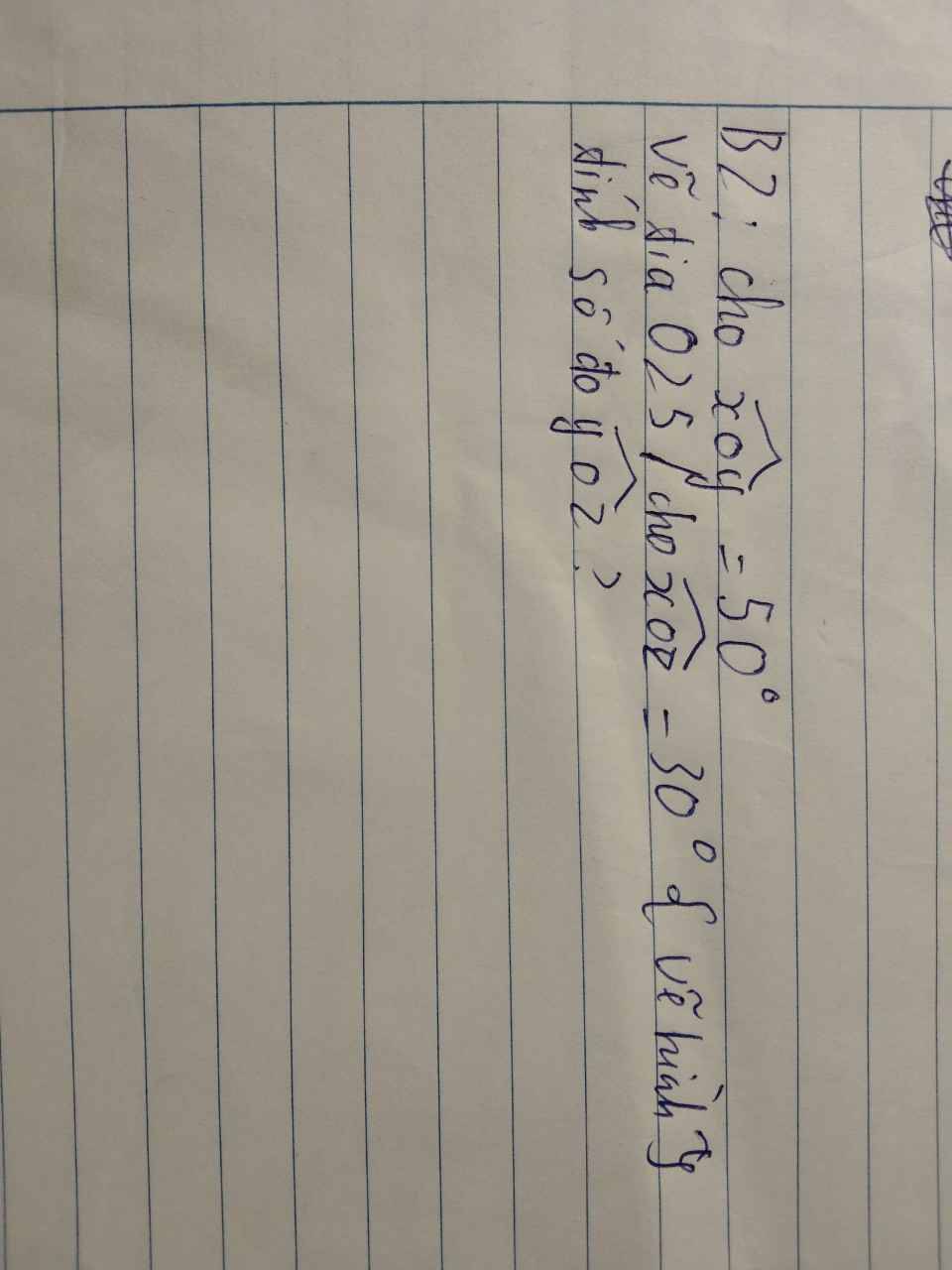Tìm các số điền vào các ô trống của trò chơi Sudoku sau:
các bạn giúp mình cái trình bày rõ ra mik tích cho plsss
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
7 tháng 4
TH1: Oz nằm giữa Ox và Oy
=>\(\widehat{xOz}+\widehat{yOz}=\widehat{xOy}\)
=>\(\widehat{yOz}+30^0=50^0\)
=>\(\widehat{yOz}=20^0\)
TH2: Ox nằm giữa Oz và Oy
=>\(\widehat{yOz}=\widehat{xOz}+\widehat{xOy}\)
=>\(\widehat{yOz}=50^0+30^0=80^0\)
T
7 tháng 4
a/ \(\dfrac{2^3\cdot3^4}{2^2\cdot3^2\cdot5}=\dfrac{2\cdot3^2}{5}=\dfrac{18}{5}\);
\(\dfrac{2^4\cdot5^2\cdot11^2\cdot7}{2^3\cdot5^3\cdot7^2\cdot11}=\dfrac{2\cdot11}{5\cdot7}=\dfrac{22}{35}\)
b/ \(\dfrac{121\cdot75\cdot130\cdot169}{39\cdot60\cdot11\cdot198}=\dfrac{11^2\cdot\left(3\cdot5^2\right)\cdot\left(2\cdot5\cdot13\right)\cdot13^2}{\left(3\cdot13\right)\cdot\left(2^2\cdot3\cdot5\right)\cdot11\cdot\left(2\cdot3^2\cdot11\right)}\)
\(=\dfrac{11^2\cdot2\cdot3\cdot5^3\cdot13^3}{11^2\cdot2^3\cdot3^4\cdot5\cdot13}=\dfrac{5^2\cdot13^2}{2^2\cdot3^3}=\dfrac{4225}{108}\)
c/ \(\dfrac{1989\cdot1990+3978}{1992\cdot1991-3984}=\dfrac{1989\cdot1990+2\cdot1989}{1992\cdot1991-2\cdot1992}\) (sửa đề)
\(=\dfrac{1989\cdot\left(1990+2\right)}{1992\cdot\left(1991-2\right)}=\dfrac{1989\cdot1992}{1992\cdot1989}=1\)
d/ \(\dfrac{125}{1000}=\dfrac{125:125}{1000:125}=\dfrac{1}{8}\);
\(\dfrac{198}{126}=\dfrac{198:18}{126:18}=\dfrac{11}{7}\);
\(\dfrac{3}{243}=\dfrac{3:3}{243:3}=\dfrac{1}{81}\);
\(\dfrac{103}{3090}=\dfrac{103:103}{3090:103}=\dfrac{1}{30}\)
QT
1
7 tháng 4
a) -22/55 = -26/65
-22/55 = -2/5
-26/65 = -2/5
Mà -2/5 = -2/5
=> 2 phân số -22/55 và -26/65 bằng nhau
b) 114/122 = 5757/6161
114/122 = 57/61
5757/6161 = 57/61
=> 2 phân số 114/122 và 5757/6161 bằng nhau
QT
3
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 4
Olm chào em, Cảm ơn em đã tin tưởng và lựa chọn gói vip của Olm. Vấn đề em hỏi, Olm xin được trả lời như sau.
Nếu đề bài cho như trên tức là em tìm trong dãy số mà đề bài đã cho các phân số thỏa mãn hai điều kiện:
Thứ nhất là mẫu của phân số đó là số tự nhiên có hai chữ số.
Thứ hai Phân số đó rút gọn thành tối giản phải bằng phân số \(\dfrac{15}{39}\);
TD
6
NQ
Nguyễn Quang Tâm
CTVHS
7 tháng 4
\(C=1+2-3-4+5+6-7-...+2014-2015-2016+2017+2018\\ C=\left(1+2-3-4\right)+\left(5+6-7-8\right)+...+\left(2013+2014-2015-2016\right)+2017+2018\\ C=\left(-4\right)+\left(-4\right)+...+\left(-4\right)+2017+2017\\ C=\left(-4\right)\cdot504+2017+2018\\ C=\left(-2016\right)+2017+2018\\ C=1+2018\\ C=2019\)
Vậy \(C=2019\)