Cho biết x và y là hai đại lượng tỉ lệ nghịch và khi x = 2, y = -15. Tìm hệ số tỉ lệ a.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sửa đề: B là giao điểm có hoành độ dương của (P) và (d)
Phương trình hoành độ giao điểm của (P) và (d):
−x² = x − 2
x² + x − 2 = 0
x² − x + 2x − 2 = 0
(x² − x) + (2x − 2) = 0
x(x − 1) + 2(x− 1) = 0
(x − 1)(x + 2) = 0
x − 1 = 0 hoặc x + 2 = 0
*) x − 1 = 0
x = 1
y = −1² = −1
B(1; −1)
*) x + 2 = 0
x = −2
y = −(−2)² = −4
A(−2; −4)
* Phương trình đường thẳng OB:
Gọi (d'): y = ax + b là phương trình đường thẳng OB
Do (d') đi qua O nên b = 0
=> (d'): y = ax
Do (d') đi qua B(1; −1) nên:
a = −1
=> (d'): y = −x
Gọi (d''): y = a'x + b' là đường thẳng đi qua A(−2; −4)
Do (d'') // (d') nên a' = −1
=> (d''): y = −x + b
Do (d'') đi qua A(−2; −4) nên:
−(−2) + b = −4
b = −4 − 2
b = −6
=> (d''): y = −x − 6

Giải:
Gọi số nhỏ thoả mãn đề bài là \(x\); \(x\) \(\in\) N
Số thứ hai là: \(x\) + 1
Số thứ ba là: \(x\) + 1 + 1
Tổng của ba số là: \(x\) + \(x\) + 1 + \(x\) + 1 + 1 = 3\(x\) + 3
Theo bài ra ta có: 3\(x\) + 3 = 483
3\(x\) = 483 - 3
3\(x\) = 480
\(x\) = 480 : 3
\(x\) = 160
Vậy số nhỏ nhất thoả mãn đề bài là: 160
Trung bình cộng của 3 số tự nhiên liên tiếp x-1,x,x+1, xϵN* là:
x = 483/3 = 161
vậy, số nhỏ nhất là 160

x;y tỉ lệ nghịch với 4;5 nên :
\(k=\dfrac{x}{4}=\dfrac{y}{5}\)
Theo TCDSTLBN ta có :
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{x+y}{4+5}=\dfrac{18}{9}=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{4}=2\\\dfrac{y}{5}=2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=8\\y=10\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(8;10\right)\)
\(\dfrac{x}{y}=\dfrac{5}{4}\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}\)
ADTC dãy tỉ số bằng nhau
\(\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{x+y}{5+4}=\dfrac{18}{9}=2\Rightarrow x=10;y=8\)

\(\left(a+2\right)\left(a+3\right)\left(a+4\right)\left(a+5\right)-24\)
\(=\left(a^2+7a+10\right)\left(a^2+7a+12\right)-24\)
Đặt a^2 + 7a = t
\(\left(t+10\right)\left(t+12\right)-24=t^2+22t+120-24\)
\(=\left(t+6\right)\left(t+16\right)\)
\(\Rightarrow\left(a^2+7a+6\right)\left(a^2+7a+16\right)=\left(a+1\right)\left(a+6\right)\left(a^2+7a+16\right)\)

Tổng giữa tử và mẫu là:
16 + 19 = 35
Khi bớt đi một số ở tử số và cộng thêm chính nó ở mẫu số thì hiệu vẫn không thay đổi, vẫn là 35
Ta có sơ đồ:
...........................
Tổng số phần bằng nhau là:
1 + 4 = 5 (phần)
Tử số mới là:
35 : 5 x 1 = 7
Số cần tìm là:
16 - 7 = 9
Đ/s: 9

a) \(\left(2x-5\right)\left(3x+b\right)=ax^2+bx+c\)
\(\Rightarrow6x^2+2bx-15x-5b=ax^2+bx+c\)
\(\Rightarrow6x^2+\left(2b-15\right)x-5b=ax^2+bx+c\)
\(\Rightarrow\left\{{}\begin{matrix}a=6\\2b-15=b\\-5b=c\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=6\\b=15\\c=-75\end{matrix}\right.\)
b) \(\left(ax+b\right)\left(x^2-x-1\right)=ax^3+cx^2-1\)
\(\Rightarrow ax^3-ax^2-ax+bx^2-bx-b=ax^3+cx^2-1\)
\(\Rightarrow ax^3-ax^2+bx^2-ax-bx-b=ax^3+cx^2-1\)
\(\Rightarrow ax^3+\left(b-a\right)x^2-\left(a+b\right)x-b=ax^3+cx^2-1\)
\(\Rightarrow\left\{{}\begin{matrix}b-a=c\\-\left(a+b\right)=0\\-b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b-a=c\\a=-b\\b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-1\\b=1\\c=2\end{matrix}\right.\)
c) \(ax\left(x-4\right)-b\left(x+6\right)+5=2x^2+5x\left(a-b\right)-6x+c\)
\(\Rightarrow ax^2-4ax-bx-6b+5=2x^2+\left(5a-5b\right)x-6x+c\)
\(\Rightarrow ax^2-\left(4a+b\right)x-\left(5a-5b\right)x-6b+5=2x^2-6x+c\)
\(\Rightarrow ax^2-\left(4a+b+5a-5b\right)x-6b+5=2x^2-6x+c\)
\(\Rightarrow ax^2-\left(9a-4b\right)x-6b+5=2x^2-6x+c\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\\-\left(9a-4b\right)=-6\\-6b+5=c\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2\\b=\dfrac{9a-6}{4}\\c=-6b+5\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=2\\b=3\\c=-13\end{matrix}\right.\)
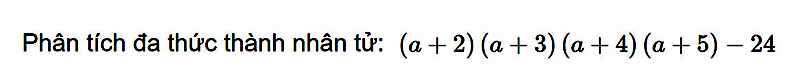
Do x và y là hai đại lượng tỉ lệ nghịch nên:
\(a=xy=2\cdot\left(-15\right)=-30\)