\(\left(2+\sqrt{5}+\sqrt{3}\right)\left(2+\sqrt{5}-\sqrt{3}\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) $n_{Na_2SO_3} = \dfrac{37,8}{126} = 0,3(mol)$
$n_{H_2SO_4} = \dfrac{200.19,6\%}{98} = 0,4(mol)$
$Na_2SO_3 + H_2SO_4 \to Na_2SO_4 + SO_2 + H_2O$
Ta thấy $n_{Na_2SO_3} : 1 < n_{H_2SO_4} :1$ nên $H_2SO_4$ dư
$n_{SO_2} = n_{Na_2SO_3} = 0,3(mol) \Rightarrow V_{SO_2} = 0,3.22,4 = 6,72(lít)$
b) $m_{dd\ sau\ pư} = 37,8 +200 - 0,3.64 = 218,6(gam)$
$n_{Na_2SO_4} = n_{H_2SO_4\ pư} = 0,3(mol) \Rightarrow n_{H_2SO_4\ dư} = 0,4 - 0,3 = 0,1(mol)$
$C\%_{Na_2SO_4} = \dfrac{0,3.142}{218,6}.100\% = 19,49\%$
$C\%_{H_2SO_4} = \dfrac{0,1.98}{218,6}.100\% = 4,48\%$



$n_{Na_2O} = \dfrac{9,3}{62} = 0,15(mol)$
$Na_2O + H_2O \to 2NaOH$
$n_{NaOH} = 2n_{Na_2O} = 0,15.2 = 0,3(mol)$
$C_{M_{NaOH}} = \dfrac{0,3}{0,4} = 0,75M$

`a)` A có nghĩa khi \(\left\{{}\begin{matrix}2ab\ge0\\\sqrt{a^2+b^2}\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a,b\ge0;a,b\le0\\a;b\ne0\end{matrix}\right.\)
\(\rightarrow\left[{}\begin{matrix}a;b>0\\a;b< 0\end{matrix}\right.\)
`b)`\(a=b\)
\(A=\left(1-\dfrac{\sqrt{2ab}}{\sqrt{a^2+b^2}}\right)\left(1+\dfrac{\sqrt{2ab}}{\sqrt{a^2+b^2}}\right)\)
\(A=1^2-\left(\dfrac{\sqrt{2ab}}{\sqrt{a^2+b^2}}\right)^2\)
\(A=1-\dfrac{2ab}{a^2+b^2}\)
\(A=1-\dfrac{2a^2}{2a^2}\)
\(A=1-1=0\)
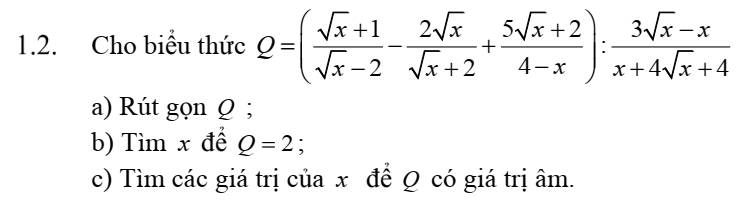
\(\left(2+\sqrt{5}+\sqrt{3}\right)\left(2+\sqrt{5}-\sqrt{3}\right)\)
\(=\left(2+\sqrt{5}\right)^2-\left(\sqrt{3}\right)^2\)
\(=4+4\sqrt{5}+5-3\)
\(=6+4\sqrt{5}\)
tổng kết quả là 14,94
5,96 x 2,5 =14,94
mình ko bt giải thích thế nào cho hiểu bạn thong cảm nhé ( tôi cúng lớp 9 )