2A - (\(xy\) + 3\(x^2\) - 2y²) = \(x^2\) - 8y² + \(xy\)

2A = \(x^2\) - 8y² + \(xy\) + \(xy\) + 3\(x^2\) - 2y²

2A = (\(x^2\) + 3\(x^2\)) - (8y² + 2y²) + (\(xy+xy\))

2A = 4\(x^2\) - 10y² + 2\(xy\)

A  = (4\(x^2\) - 10y² + 2\(xy\)): 2 

A = (2\(x^2\) - 5y² + \(xy\)).2:2

A  = 2\(x^2\) - 5y² + \(xy\)

`@` `\text {Ans}`

`\downarrow`

\((x+ 3y)(x - 2у)\)

`= x(x-2y) + 3y(x-2y)`

`= x^2 - 2xy + 3xy - 6y^2`

`= x^2 + xy - 6y^2`

   6a - [ b + 3a - (4a - b)]

= 6a - [ b + 3a - 4a + b]

= 6a - [2b - a]

= 6a - 2b + a

= 7a - 2b

YC ĐỀ LÀ GÌ EM?

tính

\(\left(x^2y-3xy^2-y^2\right)+\left(5xy^2-4y^2+5x^2y\right)\\ =\left(x^2y+5x^2y\right)+\left(-3xy^2+5xy^2\right)+\left(-y^2-4y^2\right)\\ =6x^2y+2xy^2-5y^2\)

\(\left(x^2y-3xy^2-y^2\right)+\left(5xy^2-4y^2+5x^2y\right)\\ =x^2y-3xy^2-y^2+5xy^2-4y^2+5x^2y\\ =\left(x^2y+5x^2y\right)+\left(-3xy^2+5xy^2\right)+\left(-y^2-4y^2\right)\\ =6x^2y+2xy^2-5y^2\)

Đề bài phải sửa thành "biết AD=AB" mới làm được

a/

ABCD là hình thàng cân => AD=BC

Mà AD=AB (gt)

=> AD=BC

b/

ABCD là hình thang cân

\(\Rightarrow\widehat{BAD}=\widehat{ABC}\)

\(\widehat{BCD}+\widehat{ABC}=180^o\) (Hai góc trong cùng phía)

\(\Rightarrow\widehat{BCD}+\widehat{BAD}=180^o\)

=> ABCD là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bù nhau là tứ giác nt)

Ta có

Cung AB và cung BC có hai dây trương cung bằng nhau

AB=BC (cmt) => sđ cung AB = sđ cung BC (1)

\(sđ\widehat{ADB}=\dfrac{1}{2}sđcungAB\) (góc nội tiếp) (2)

\(sđ\widehat{CDB}=\dfrac{1}{2}sđcungBC\) (góc nội tiếp) (3)

Từ (1) (2) (3) \(\Rightarrow\widehat{ADB}=\widehat{CDB}\) => DB là phân giác của \(\widehat{ADC}\)

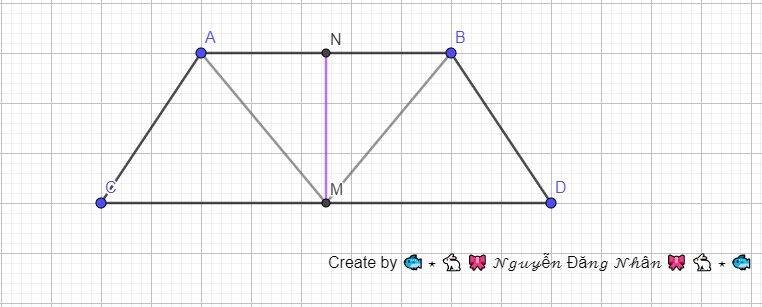
a) Xét 2 tam giác AMC và BMD có:

\(\widehat{C}=\widehat{D}\) (góc kề một đáy)

\(AC=BD\) (cạnh bên)

\(MC=MD\) (giả thiết)

\(\Rightarrow\Delta AMC=\Delta BMC\) (cạnh.góc.cạnh)

\(\Rightarrow AM=BM\)

b) Xét 2 tam giác NMA và NMB có:

\(NA=NB\) (giả thiết)

\(NM\): cạnh chung

\(MA=MB\) (chứng minh trên)

\(\Rightarrow\Delta NMA=\Delta NMB\)

\(\Rightarrow\widehat{MNA}=\widehat{MNB}\)

Mà 2 góc \(\widehat{MNA}=\widehat{MNB}\) là 2 góc kề bù, nên:

\(\widehat{MNA}=\widehat{MNB}=\dfrac{180^o}{2}=90^o\)

Vậy MN là đường cao:

1) dư số 9 trước dấu lớn và cái (2) mình xin sửa đề là \(\ge3\).. mới làm được ấy: )

1)

`=>3(2x+1)-2(x-2)>18(x-3)`

`<=>6x+3-2x+4>18x-54`

`<=>-14x>-61`

`=>x<61/14`

2)

`=>12x-3(x-3)>=36-(x-3)`

`<=>12x-3x+9>=36-x+3`

`<=>10x>=30`

`<=>x>=3`

`=> T:3<=x<61/14`

Mà x là các giá trị nguyên nên x thuộc {3; 4}

a) \(\left(x+3\right)^2-x\left(x-1\right)=2\)

\(\Leftrightarrow x^2+6x+9-x^2+x=2\)

\(\Leftrightarrow7x+9=2\)

\(\Leftrightarrow7x=2-9\)

\(\Leftrightarrow7x=-7\)

\(\Leftrightarrow x=\dfrac{-7}{7}=-1\)

b) \(\left(2x+3\right)^2-\left(x+1\right)\left(4x-3\right)=-1\)

\(\Leftrightarrow4x^2+12x+9-\left(4x^2-3x+4x-3\right)=-1\)

\(\Leftrightarrow4x^2+12x+9-4x^2+3x-4x+3=-1\)

\(\Leftrightarrow11x+12=-1\)

\(\Leftrightarrow11x=-13\)

\(\Leftrightarrow x=\dfrac{-13}{11}\)

Nguyên tố X có tổng số hạt trong nguyên tử bằng 40, ta có:

\(p+e+n=2p+n=40\left(1\right)\)

Trong nguyên tử X số hạt mang điện nhiều hơn số hạt không mang điện là 12, ta có:

\(2p-n=12\left(2\right)\)

Từ (1), (2) có hệ phương trình: \(\left\{{}\begin{matrix}2p+n=40\\2p-n=12\end{matrix}\right.\)

\(\Leftrightarrow4p=52\Rightarrow p=\dfrac{52}{4}=13\)

Tên của nguyên tố X là nhôm (Al).

(1) \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)

(2) KNO3 không nhiệt phân được, bạn xem lại đề nhé: )

Ta có các hạt của nguyên tô X là: \(p+e+n=40\)

Mà: \(e=p=2p\Rightarrow2p+n=40\)(1)

Số hạt mang điện nhiều hơn số hạt không mang điện là 12

Ta có: \(2p-n=12\) (2)

Từ (1) và (2) ta có hệ:

\(\left\{{}\begin{matrix}2p+n=40\\2p-n=12\end{matrix}\right.\)

Giải hệ ta tìm được: \(p=e=13\)

Và \(n=14\)

\(\Rightarrow X\) là \(Al\)

(1) \(2Al+6HCl\rightarrow2AlCl_3+3H_2\uparrow\)

\(\Rightarrow A\) là \(H_2\)

(2) \(2KNO_3\xrightarrow[]{t^o}2KNO_2+O_2\uparrow\) 

\(\Rightarrow Y\) là \(O_2\)

(3) \(2H_2+O_2\xrightarrow[]{t^o}2H_2O\)

\(\Rightarrow B\) là \(H_2O\)

(4) \(2H_2O+Ca\rightarrow Ca\left(OH\right)_2+H_2\)

\(\Rightarrow\) D là \(Ca\left(OH\right)_2\)