Có a + b +c =0

 <=> a + b = -c

=> a²+b²+2ab = c² 

=> a²+b² -c² = -2ab

=>(  a²+b² -c²) = 4a²b²

<=> a⁴ +b⁴ +c⁴+2a²b^2-2b²c²-2a²c²=4a²b²

=> a⁴+b⁴+c⁴= 2a²b²+2b²c²+2c²a²

=> 2(a⁴+b⁴+c⁴)=2a²b²+2b²c²+2c²a²+a⁴+b⁴+c⁴

<=> 2(a⁴+b⁴+c⁴)=(a²+b²+c²)²

<=>a⁴+b⁴+c⁴= \(\dfrac{\left(a^2+b^2+c^2\right)^2}{2}=\dfrac{1^2}{2}=\dfrac{1}{2}\)

Ta có

\(\left(a+b+c\right)^2=a^2+b^2+c^2+2ab+2bc+2ac=0\)

\(\Rightarrow2\left(ab+bc+ac\right)=-1\Rightarrow ab+bc+ac=-\dfrac{1}{2}\)

Ta có

\(\left(a^2+b^2+c^2\right)^2=a^4+b^4+c^4+2a^2b^2+2b^2c^2+2a^2c^2=1\)

\(\Rightarrow a^4+b^4+c^4=1-2\left(a^2b^2+b^2c^2+a^2c^2\right)\) (1)

Ta có

\(\left(ab+bc+ac\right)^2=a^2b^2+b^2c^2+a^2c^2+2ab^2c+2abc^2+2a^2bc=\dfrac{1}{4}\)

\(\Rightarrow a^2b^2+b^2c^2+a^2c^2+2abc\left(b+c+a\right)=\dfrac{1}{4}\)

\(\Rightarrow a^2b^2+b^2c^2+a^2c^2=\dfrac{1}{4}\) Thay vào (1)

\(\Rightarrow a^4+b^4+c^4=1-2\left(a^2b^2+b^2c^2+a^2c^2\right)=1-2x\dfrac{1}{4}=\dfrac{1}{2}\)

Bạn cần hỗ trợ bài nào thì nên ghi chú rõ ra.

Đề như này đúng không bạn

\(A=\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{x+z}\)

 áp dụng bất đẳng thức bunhia dạng phân thức có 

  \(\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}\ge\dfrac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\dfrac{3^2}{2\cdot3}=\dfrac{3}{2}\)

Dấu ''='' xay ra khi x=y=z=1

Vậy Amin=3/2 khi x=y=z=1

\(A=\Sigma\dfrac{x^2}{x+y}\ge\dfrac{\left(x+y+z\right)^2}{x+y+y+z+x+z}=\dfrac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\dfrac{3^2}{2.3}=\dfrac{3}{2}\)

\(dấu"="\Leftrightarrow x=y=z=1\)

đề thế này à bạn nãy mình đọc chắc nhầm

\(\Sigma\dfrac{a}{ab+1}=a-\dfrac{a^2b}{ab+1}\ge\Sigma a-\dfrac{a^2b}{2\sqrt{ab}}=\Sigma a-\dfrac{a\sqrt{ab}}{2}\)

\(\Rightarrow\Sigma\dfrac{a}{ab+1}\ge a+b+c-(\dfrac{a\sqrt{ab}}{2}+\dfrac{b\sqrt{bc}}{2}+\dfrac{c\sqrt{ca}}{2})\)

\(=3-\dfrac{1}{2}\left(\Sigma a\sqrt{ab}\right)\ge3-\dfrac{1}{2}\left(\dfrac{a\left(a+b\right)}{2}+\dfrac{b\left(b+c\right)}{2}+\dfrac{c\left(c+a\right)}{2}\right)=3-\dfrac{1}{4}\left(a^2+b^2+c^2+ab+bc+ca\right)=3-\dfrac{1}{4}\left[\left(a+b+c\right)^2-\left(ab+bc+ca\right)\right]\ge3-\dfrac{1}{4}\left[3^2-\dfrac{\left(a+b+c\right)^2}{3}\right]=3-\dfrac{1}{4}\left[3^2-\dfrac{3^2}{3}\right]=\dfrac{3}{2}\)

\(dấu"="\Leftrightarrow a=b=c=1\)

\(B=\Sigma\dfrac{1}{b+1}\ge\dfrac{9}{a+b+c+1+1+1}=\dfrac{9}{3+3}=\dfrac{3}{2}\)

\(dấu"="\Leftrightarrow a=b=c=1\)

a) Vì số hạng thứ nhất tăng 25 đơn vị, số hạng thứ hai giữ nguyên

=> Tổng hai số tăng 25 đơn vị => 101 + 25 = 126.

b) Vì mỗi số hạng tăng lên 19 đơn vị

=> Tổng hai số tăng lên 19 + 19 = 38 đơn vị => 101 + 38 = 139.

c) Vì mỗi số hạng giảm 8 đơn vị

=> Tổng hai số giảm xuống 8 + 8 = 16 đơn vị => 101 - 16 = 85.

d) Vì số hạng thứ nhất giữ nguyên, số hạng thứ hai tăng 33 đơn vị

=> Tổng hai số tăng lên 33 đơn vị => 101 + 33 = 134.

e) Vì số hạng thứ nhất tăng 89 đơn vị, số hạng thứ hai giảm 98 đơn vị

=> Tổng hai số tăng 89 đơn vị, rồi lại giảm xuống 98 đơn vị => 101 + 89 - 98 = 92.

Để giải dạng bài này ta phải quy các góc về 1 duy nhất ví dụ quy tất cả ra góc A

có: 2A = 3B => B=2A/3

2A = 4C => C= 2A/4= A/2

2A=6D => D=2A/6 = A/3

A+B+C+D = A + 2A/3 + A/2 + A/3

=A(1+2/3 + 1/2 + 1/3)

=5A/2 = 360 độ

=> A = 360x2/5 = 144 độ

B =2A/3 = 2x144/3= 96 độ

C = A/2 = 144/2 = 72 độ

D=  A/3 = 144/3 = 48 độ

Mọi thắc mắc tới toán có thể liên hệ để được giải đáp thêm

Nửa chu vi hcn là: `78:2=39(m)`

Gọi chiều dài hcn ban đầu là: `x (m)`       `ĐK: 3 < x < 39`

`=>` Chiều rộng hcn ban đầu là: `39-x(m)`

Vì nếu giảm chiều dài `3` đơn vị chiều rộng tăng `4` đơn vị thì hcn thành hvg nên ta có ptr:

       `x-3=39-x+4`

`<=>2x=46`

`<=>x=23` (t/m)

Vậy diện tích hcn ban đầu là: `23.(39-23)=368 m^2`

Nửa chu vi hcn là: $78:2=39\left(m\right)$

Gọi chiều dài hcn ban đầu là: $x\left(m\right)$       $ĐK:3<x<39$

$\Rightarrow$ Chiều rộng hcn ban đầu là: $39-x\left(m\right)$

Vì nếu giảm chiều dài $3$ đơn vị chiều rộng tăng $4$ đơn vị thì hcn thành hvg nên ta có ptr:

       $x-3=39-x+4$

$\iff 2x=46$

$\iff x=23$ (t/m)

Vậy diện tích hcn ban đầu là: $23.(39-23)=368m^2$

`(4x^2-4x+1)-(x+1)^2`

`=(2x-1)^2-(x+1)^2`

`=(2x-1-x-1)(2x-1+x+1)`

`=(x-2).3x`

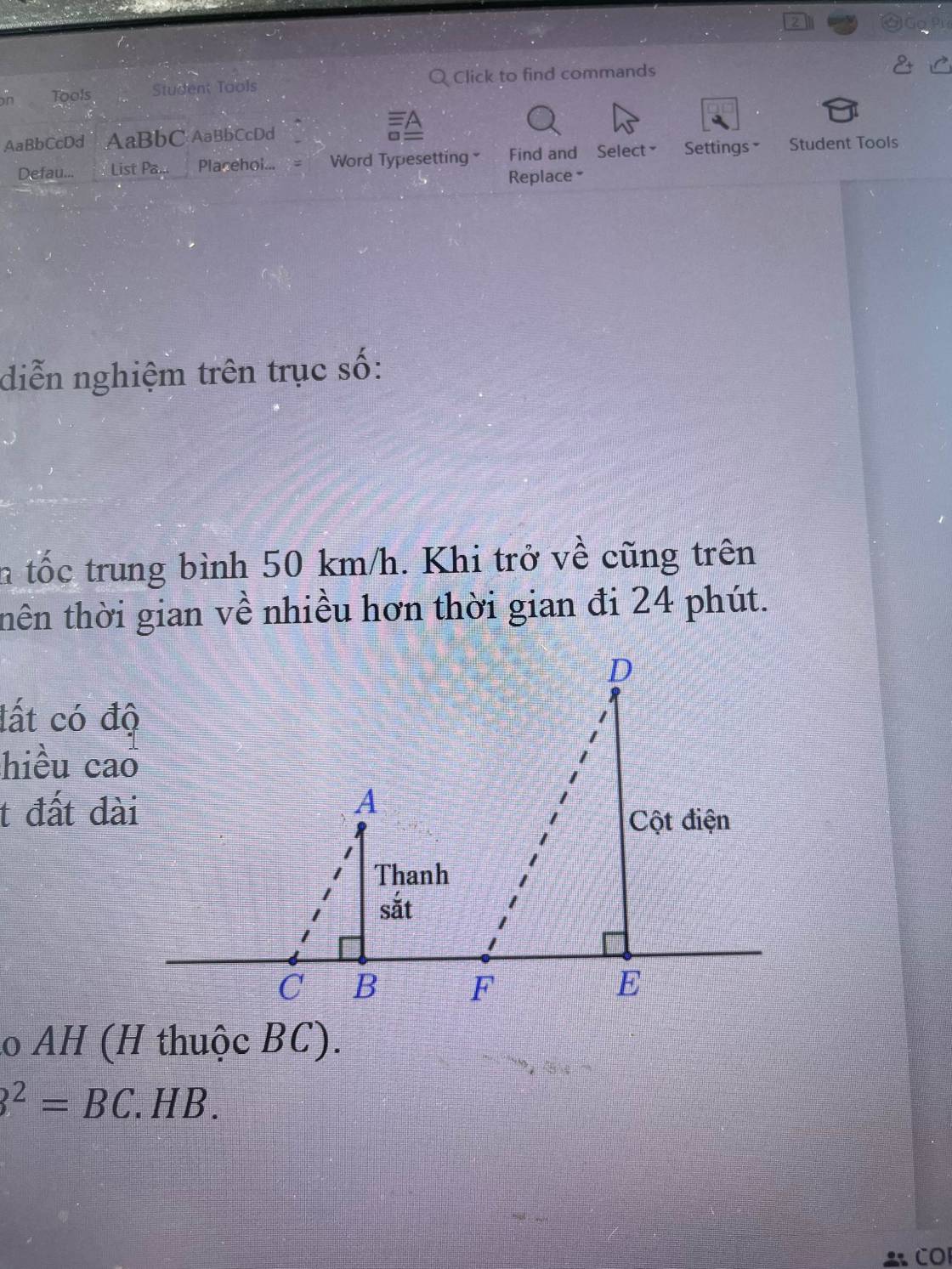
Do các tia sáng được coi là song song nên ta có \(AC//DF\Rightarrow\widehat{ACB}=\widehat{DFE}\) (hai góc đồng vị)

Ta có: \(EF=1,6m;AB=1,8m;BC=0,4m\)

Xét \(\Delta ABC\) và \(\Delta DEF\) có:

\(\widehat{ABC}=\widehat{DEF}=90^0;\widehat{ACB}=\widehat{DFE}\)

\(\Rightarrow\Delta ABC\sim\Delta DEF\) (g.g)

\(\Rightarrow\dfrac{AB}{BC}=\dfrac{DE}{EF}\Rightarrow DE=\dfrac{AB.EF}{BC}=\dfrac{1,8.1,6}{0,4}=7,2\left(m\right)\)

Vậy chiều cao cột điện là \(7,2m\).

Vì `AB //// DE=>\hat{ACB}=\hat{DFE}` (`2` góc đồng vị)

Xét `\triangle ABC` và `\triangle DEF` có:

    `{(\hat{ACB}=\hat{DFE}),(\hat{ABC}=\hat{DEF}(=90^o)):}`

  `=>\triangle ABC` $\backsim$ `\triangle DEF` (g-g)

   `=>[AB]/[BC]=[DE]/[EF]`

   `=>[1,8]/[0,4]=[DE]/[1,6]`

   `=>DE=7,2(m)` là chiều cao của cột điện

Hình thang ABCD có hai cạnh bên AD=BC nên nó là hình thang cân

Vậy \(\widehat{D}=\widehat{C}\)