a. Ta có: OB = OD (tính chất hình bình hành)

\(OE=\frac{1}{2}OD\left(GT\right)\)

\(OF=\frac{1}{2}OB\left(GT\right)\)

Suy ra: OE = OF

Xét tứ giác AECF, ta có:

OE = OF (chứng minh trên)

OA = OC (vì ABCD là hình bình hành)

Suy ra: Tứ giác AECF là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường ) ⇒ AE // CF

b. Kẻ OM // AK

Trong ∆ CAK ta có:

OA = OC ( chứng minh trên)

OM // AK ( theo cách vẽ)

⇒ CM // MK (tính chất đường trung bình của tam giác) (1)

Trong ∆ DMO ta có:

DE = EO (gt)

EK // OM

⇒ DK // KM (tính chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: DK = KM = MC ⇒ DK =\(\frac{1}{2}KC\)

Vào TKHĐ là thấy hình :)

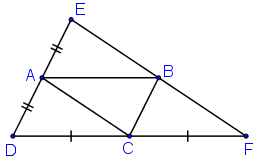
Ta có: ABCD là hình bình hành nên AB //= CD, AD//=BC.

+ E đối xứng với D qua A

⇒ AE = AD

Mà BC = AD

⇒ BC = AE.

Lại có BC // AE (vì BC // AD ≡ AE)

⇒ AEBC là hình bình hành

⇒ EB //= AC (1).

+ F đối xứng với D qua C

⇒ CF = CD

Mà AB = CD

⇒ AB = CF

Mà AB // CF (vì AB // CD ≡ CF)

⇒ ABFC là hình bình hành

⇒ AC //= BF (2)

Từ (1) và (2) suy ra E, B, F thẳng hàng và BE = BF

⇒ B là trung điểm EF

⇒ E đối xứng với F qua B

x(x² + x + 1) = 4y(y + 1)

<=> (x + 1)(x² + 1) = (2y + 1)²

Dễ dàng thấy là: x + 1 và x² + 1 nguyên tố cùng nhau nên x + 1 và x² + 1 là 2 số chính phương.

=> x²; x² + 1 là 2 số chính phương liên tiếp 

=> x = 0; y = 0 hoặc y = - 1

đặt 8xy lm chung nhe bn 

=8xy(8-12x+6x²-x²)

\(a^3-a\)

\(=a\left(a^2-1\right)\)

\(=a\left(a^2-1^2\right)\)

\(=a\left(a-1\right)\left(a+1\right)\)

mà a và a - 1 và a + 1 là 3 số liên tiếp

Ta có tích 3 số liên tiếp luôn chia hết cho 6

\(\Rightarrow a^3-a⋮6\left(đpcm\right)\)

a) A = x^2 -10x + 27
Ta có:
A = x^2 - 10x + 27
   = x^2 - 2.x.5 + 5^2  + 2
   = (x-5)^2 + 2
Do (x-5)^2 > 0 ( với mọi x )
=> (x-5)^2 + 2 > 2 (với mọi x)
=> Amin = 2
Dấu "=" xãy ra khi và chỉ khi x-5=0  <=> x=5
Vậy : GTNN của A bằng 2 tại x = 5

b, B = 4x^2 + 4x + 20
Ta có :
 B = 4x^2 + 4x + 20
     = (2x)^2 + 2.2x.1 + 1^2 + 19
     = (2x+1)^2  + 19
Do (2x+1)^2 > 0 ( với mọi x)
=> (2x+1)^2 + 19 > 19 (với mọi x)
=> B > 19 (mọi x)
=> Bmin = 19
Dấu "=" xãy ra <=> 2x+1 = 0
<=> x = -1/2
Vậy : GTNN của B =19 tại x = -1/2

đặt 3 xy làm chung nha bn ...

~ hok tốt ~

chung 3xy nhek

A = 4x - x² + 5

A = - (x² - 4x + 4 ) +1

A = - ( x -2 )² + 1

Do - (x - 2 )²  <= 0 

=>  A <= 1 

Dấu "=" xảy ra khi x -2 =0

<=> x = 2

 Vậy A min = 1 khi x =2 

\(A=4x-x^2+5=-\left(x^2-4x-5\right)=-\left(x^2-4x+4-9\right)=-\left(x-2\right)^2+9\le9\forall x\)

dấu = xảy ra khi: \(-\left(x-2\right)^2=0\Rightarrow x=2\)

Vậy Max A = 9 tại x = 2

\(B=x-x^2=-\left(x^2+x\right)=-\left(x^2+x+\frac{1}{4}-\frac{1}{4}\right)=-\left(x+\frac{1}{2}\right)^2+\frac{1}{4}\le\frac{1}{4}\forall x\)

dấu = xảy ra khi: \(-\left(x+\frac{1}{2}\right)^2=0\Rightarrow x=-\frac{1}{2}\)

Vậy Max B = 1/4 tại x= -1/2

=.= hok tốt!!

\(xy-5y-5x+x^2=\left(x^2+xy\right)-\left(5x+5y\right)=x\left(x+y\right)-5\left(x+y\right)=\left(x+y\right)\left(x-5\right)\)

=.= hok tốt!!

\(xy-5y-5x+x^2\)

\(=y\left(x-5\right)-x\left(5-x\right)\)

\(=y\left(x-5\right)+x\left(x-5\right)\)

\(=\left(x-5\right)\left(y+x\right)\)