Tìm giá trị nhỏ nhất của:
A=x^2-5x+4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bạn đăng tách ra nhé
a, \(x-\dfrac{3}{7}=\dfrac{1}{8}\Leftrightarrow x=\dfrac{1}{8}+\dfrac{3}{7}=\dfrac{31}{56}\)
b, \(-2x=\dfrac{1}{6}+\dfrac{3}{5}=\dfrac{23}{30}\Leftrightarrow x=\dfrac{23}{30}:\left(-2\right)=-\dfrac{23}{-60}\)
c, \(\left|2x-3\right|=\dfrac{1}{6}-\dfrac{1}{2}=\dfrac{-1}{3}\)( vô lí )

a + b, A=\(\dfrac{x-3\sqrt{x}+2}{x-4\sqrt{x}+3}\) = \(\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-3\right)}\)=\(\dfrac{\sqrt{x}-2}{\sqrt{x}-3}\)
ĐKXĐ: \(\sqrt{x}-3\)\(\Leftrightarrow\sqrt{x}\)\(\ne\)3\(\Leftrightarrow\) x\(\ne\)9
c, \(\dfrac{\sqrt{x}-2}{\sqrt{x}-3}=\dfrac{\sqrt{x}-3+1}{\sqrt{x}-3}=1+\dfrac{1}{\sqrt{x}-3}\Rightarrow\sqrt{x}-3\inƯ\left(1\right)=\left\{\pm1\right\}\)
| \(\sqrt{x}-3\) | 1 | -1 |
| x | 16 | 4 |




Ta có : (x×2+x)×2-14(x×2+x)+24
= 3x×2-14×3x+24
= 6x-42x+24
= 24-36x
= 6(4-6x)

\(\dfrac{-x^{2n}y^{2n-1}}{\dfrac{1}{5}x^{2n-1}y^{2n-4}}=-5x^{-1}y^3=-\dfrac{1}{5}xy^3\)
 ai
ai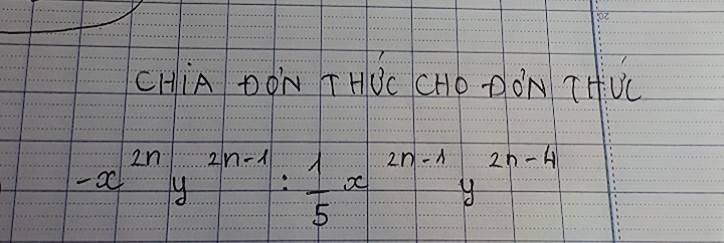
\(A=x^2-2.\dfrac{5}{2}x+\dfrac{25}{4}-\dfrac{9}{4}=\left(x-\dfrac{5}{2}\right)^2-\dfrac{9}{4}\ge-\dfrac{9}{4}\)
\(A_{min}=-\dfrac{9}{4}\) khi \(x=\dfrac{5}{2}\)
\(A=x^2-5x+4\)
\(\Leftrightarrow A=x^2-2.x.\dfrac{5}{2}+\left(\dfrac{5}{2}\right)^2-\dfrac{9}{4}\)
\(\Leftrightarrow A=\left(x-\dfrac{5}{2}\right)^2-\dfrac{9}{4}\ge-\dfrac{9}{4}\)
Dấu bằng xảy ra
\(\Leftrightarrow x-\dfrac{5}{2}=0\)
\(\Leftrightarrow x=\dfrac{5}{2}\)